Data Structure
This document outlines the fundamental data structure in Java. The most commonly used data structures in Java include ArrayList, HashMap, Queue, Stack, and BST (Binary Search Tree). These data structures are clearly different but have some relationship. The following scheme exhibits the relationship of these data structures. Notice that some are Interface and some are Class.

Abstract Data Types (ADT) vs. interface
An abstract data type is a self-contained, user-defined type that bundles data with a set of related operations 1. ADT can be classified as built-in and user-defined or as mutable or immutable 2. For example, the List interface is a Java built-in ADT, which defines a data structure with set of methods to operate on but without providing detailed implementation.
My own understanding of ADT is that it is a general concept, and interfaces in Java is in-built ADT for convenience for users.
Implementing an ADT in Java involves two steps. The first step is the definition of a Java Application Programming Interface (API), for interface for short, which describes the names of the methods that the ADT supoorts and how they are to be declared and used. Secondly, we need to define exceptions for any error conditions that can arise during operations 3. Java libraty provides various ADTs such as List, Stack, Queue, Set, Map as inbuilt interfaces that we implement using various data structures.
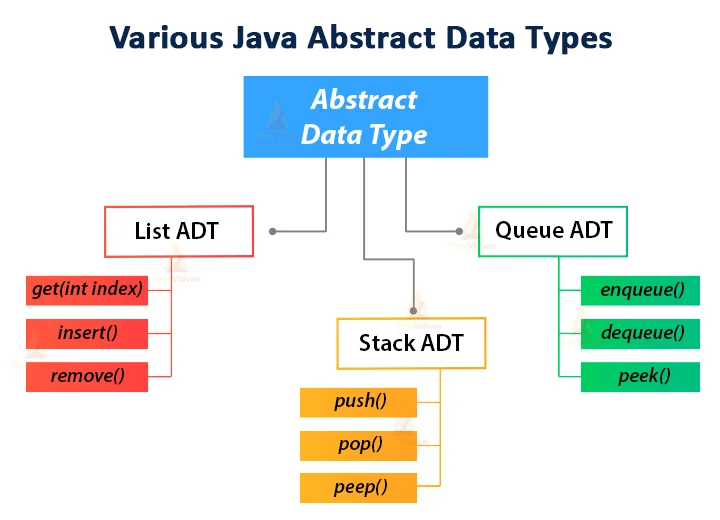
Collecction
Java Collection interface provides a architecture to store and manipulate a group of objects. The java.util package contains all the classes and interfaces for the Collection framework. The Collection interface is implemented by all the classes in the framework, and it only declares the method that each collection will have.

List
List interface extends Collection interface, which stores a list type data structure in which we can store an ordered collection of objects, and can have duplicate values. List interface is implemented by the classes ArrayList, LinkedList, Vector and Stack.
ArrayList
uses a resieable array to store objects, built on top of array. The size, isEmpty, get, set and iterator operations run in constant time, while the add operation runs in amortized constant time. Other operations roughly run in linear time, and the constant factor is low compared to LinkedList.

LinkedList
a linear data structure that consists of nodes holding a data field and a reference to another node. It is a doubly-linked list implementing both List and Deque interface. Some commonly used methods and their corresponding run time complexity are listed below:
-
.add(): add element to the end of the list and run time is constant O(1). -
.get(): get a specific element by traversing nodes one by one, and the worst run time is O(n). -
.remove(element): remove an element with runtime O(n).
In general, except for add, other LInkedList operations run in linear time.
LinkedList implementing Deque interface, which is extended Queue interface, can retrive the first element and remove it from the list, i.e., linkedList.poll() and linkedList.pop(). Also, this linkedlist can also add an element to the head like a stack, i.e., linkedList.push(e).
Stack
a generic, linear data structure that represents a Last-In-First-Out(LIFO) collection of objects. It allows to push/pop element in a constant time. Stack is a direct class of Vector, which is a synchronized implementation. A more complete and consistent set of LIFO stack operations is provided by the Deque interface, which can be implemeneted by ArrayDeque, e.g., Deque<Integer> stack = new ArrayDeque<Integer>().
Stack is also an ADT, and it can be implemented using Array, ArrayDeque and a Generic LinkedList.
Queue
a interface following First-In-First-Our (FIFO) principle typically. Except for priority queue, it order elements according to a supplied comparator or the element's natural ordering. Regardless of ordering, .remove() or .poll()operations will remove an element from the head of the queue (so called dequeue), and new element will be inserted at the tail of the queue (enqueue).
Deque
a linear collection (interface) that supports element insertion and removal at both ends, for example, addFirst() and addLast(). The Deque interface extends Queue.
-
When
Dequeis used as a queue, the collection follows FIFO manner, in which TheaddLast()operation is equivalent toadd()in queue method. -
Dequecan also be used as LIFO stacks, in which insertion and remove will be operated at the beginning of the deque. Thepopandpushoperations will be equivalent toremoveFirstandaddFirst, respectively, in deque.
Unlike the List interface, the Deque interface does not provide support for indexed access to element.
Tree
Tree structure and composition
Tree data structure
All the above mentioned data structures are linear, whereas Tree is a non-linear data structure. Tree is composed of a set of nodes, and each node store data of any types and a node pointing to its child nodes. The components and parameters of a tree is depicted below.
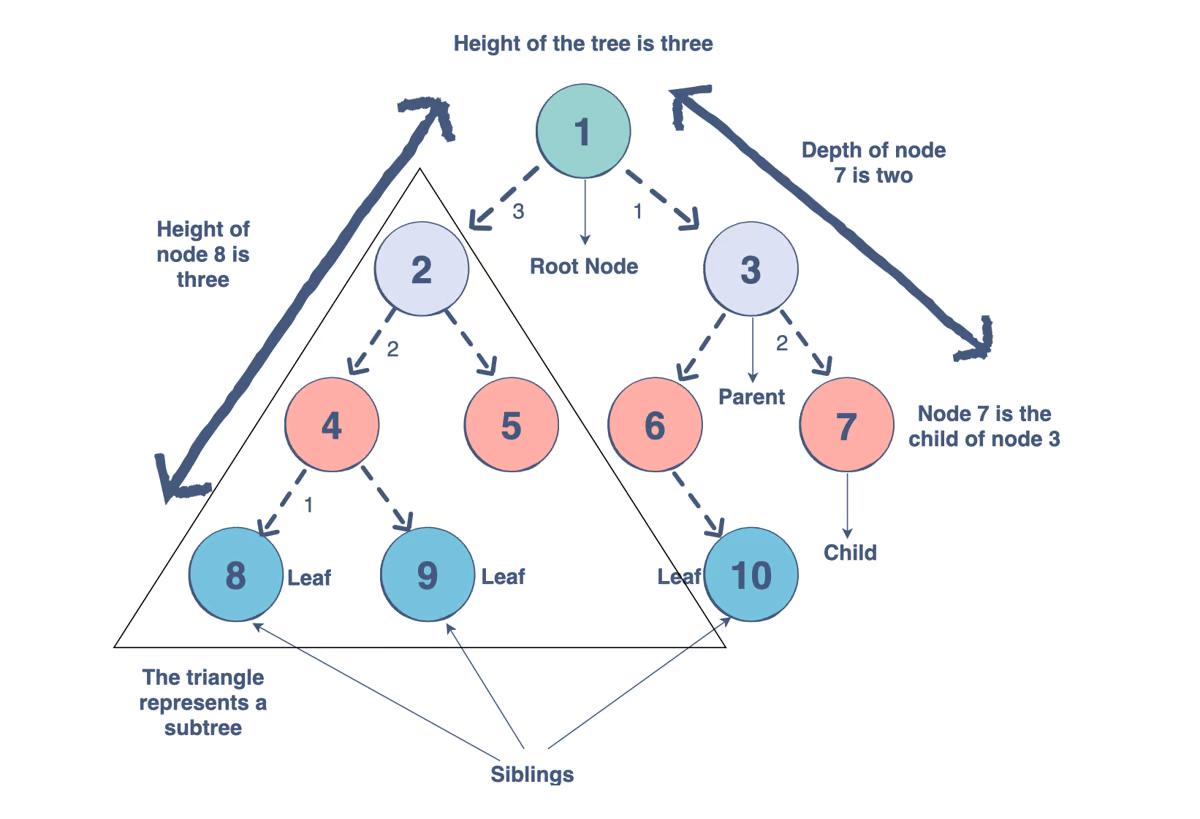
Types of trees: Binary Tree, Binary Search Tree (BST), Red-Black Tree (RBT), 2-3 Tree, 2-3-4 Tree and so on.
Applications with Tree
-
Storing hierarchy information, such file systems
-
Searching: Tree is more efficienct for searching than LinkedList
-
Inheritance: Trees are used for inheritance, XML parser, machine learning, and DNS, amongst many other things.
-
Indexing: Advanced types of trees, like B-Trees and B+ Trees, can be used for indexing a database.
and more ...
Treversal
There are two ways to traverse all nodes in a tree: Depth-First Traversal (DFT, 深度优先游历) and Breadth-First Traversal (BFT, 深度优先游历).
Depth-First Traversal (DFT)
Usually implemented by stack if using iteration.
-
Preorder: visit node, go left, go right
An illustration of the reorder traversal using stack data structure is shown below.

The corresponding codes are:
public static ArrayList<Integer> preOrderTraversalStack(TreeNode<Integer> root) { // create a new ArrayList to store values ArrayList<Integer> li = new ArrayList<>(); if (root == null) return li; // as it is DFT, uses stack Stack<TreeNode<Integer>> stack = new Stack<>(); stack.push(root); while (!stack.isEmpty()) { TreeNode<Integer> node = stack.pop(); // add node value to the list before push child nodes to the stack li.add(node.val); // due to FILO manner, push right child node in order to get the left child node if (node.right != null) stack.push(node.right); if (node.left != null) stack.push(node.left); } return li; }A more general method using Stack and Iteration:
public static List<Integer> preorderTraversalIter2(TreeNode<Integer> root) { List<Integer> list = new ArrayList<>(); Stack<TreeNode<Integer>> stack = new Stack<>(); TreeNode<Integer> node = root; while (node != null || !stack.empty()) { if (node != null) { stack.push(node); // add to the list once traverse on it list.add(node.val); node = node.left; } else { node = stack.pop(); node = node.right; } } return list; }Using recursion to implement preorder traversal:
public static ArrayList<Integer> preOrderTraversalRec(TreeNode<Integer> root) { // create a new ArrayList to store values ArrayList<Integer> li = new ArrayList<>(); if (root == null) return li; helperRecursion(root, li); return li; } private static void helperRecursion(TreeNode<Integer> root, ArrayList<Integer> li) { if (root == null) return; // Step 1: add node value to the list li.add(root.val); // Step 2: go left helperRecursion(root.left, li); // Step 3: go right helperRecursion(root.right, li); } -
Inorder: go left, visit node, go right
An illustration of the inorder traversal using stack data structure is shown below.

The corresponding implementation using stack is as follows:
public static List<Integer> inorderTraversalStack(TreeNode<Integer> root) { List<Integer> list = new ArrayList<>(); Stack<TreeNode<Integer>> stack = new Stack<>(); TreeNode<Integer> currNode = root; while(currNode!=null || !stack.empty()){ // traverse along the left edge to the bottom if (currNode != null) { stack.push(currNode); currNode = currNode.left; } else { // pop each node from the stack and add value to the list currNode = stack.pop(); list.add(currNode.val); // push the right child node if exists currNode = currNode.right; } } return list; }Recursion method:
public static ArrayList<Integer> inOrderTraversalRec(TreeNode<Integer> root) { ArrayList<Integer> li = new ArrayList<>(); helperRecusion(root, li); return li; } private static void helperRecusion(TreeNode<Integer> root, ArrayList<Integer> li) { if (root == null) return; helperRecusion(root.left, li); li.add(root.val); helperRecusion(root.right, li); } -
Postorder: go left, go right, visit node
An illustration of the postorder traversal using stack data structure is shown below.

An example code for implementation of postorder traversal shows as follows
// method 1: Normal iteration public List<Integer> postorderTraversalStack(TreeNode root) { Stack<TreeNode> stack = new Stack<>(); LinkedList<Integer> li = new LinkedList<>(); TreeNode node = root; while (node != null || !stack.isEmpty()) { while (node != null) { stack.push(node); node = node.left; } // unlike inorder traversal, here we only "peek" the node in the stack // as we need to check if it has right child node node = stack.peek(); // if it has, then traverse to the right child node if (node.right != null) { node = node.right; } else { // if it does not have, add this node value to the list node = stack.pop(); li.add(node.val); // check if this node is a right child node // if it is, pop out the node and add the value to the list while (!stack.isEmpty() && node == stack.peek().right) { node = stack.pop(); li.add(node.val); } node = null; } } return li; } // method 2: reverse preorder traversal public static List<Integer> postorderTraversalStackRev(TreeNode<Integer> root) { Stack<TreeNode<Integer>> stack = new Stack<>(); LinkedList<Integer> li = new LinkedList<>(); TreeNode<Integer> node = root; while(node != null || !stack.isEmpty()) { if (node != null) { stack.push(node); // to reverse preorder traversal, // add the value of each node traversed to the head of the list li.addFirst(node.val); // until the right side bottom node = node.right; } else { node = stack.pop(); node = node.left; } } return li; }Recursion method:
public static List<Integer> postorderTraversalRec(TreeNode<Integer> root) { List<Integer> li = new ArrayList<>(); helperRecursion(root, li); return li; } private static void helperRecursion(TreeNode<Integer> root, List<Integer> li) { if (root == null) return; helperRecursion(root.left, li); helperRecursion(root.right, li); li.add(root.val); }
Breadth-First Traversal (BFT)
-
Levelorder traversal: usually uses Queue to implement.
The following example returns a list of node values via BFT using iteractive method.
public static List<Integer> levelOrderStack(TreeNode<Integer> root) { List<Integer> li = new ArrayList<>(); if (root == null) return li; Queue<TreeNode<Integer>> queue = new LinkedList<>(); TreeNode<Integer> node = root; queue.add(node); while (!queue.isEmpty()) { node = queue.poll(); li.add(node.val); if (node.left != null) queue.add(node.left); if (node.right != null) queue.add(node.right); } return li; }Here is another example to re the node values level by level by store the node values in list and append each list to a list of lists. The main difference from the above example is that we add an extra variable
levelto track which level of the node is.public static List<List<Integer>> levelOrderLists(TreeNode<Integer> root) { List<List<Integer>> results = new ArrayList<>(); // a queue to place each node traversed Queue<TreeNode<Integer>> queue = new LinkedList<>(); if (root == null) return results; TreeNode<Integer> node = root; // add a variable to track level queue.add(node); while (!queue.isEmpty()) { List<Integer> li = new ArrayList<>(); int level = queue.size(); // add the value of the nodes in certain level to the corresponding list for (int i = 0; i < level; i++) { node = queue.remove(); li.add(node.val); // if the node has child nodes, then add the child node to the queue and increase the level if (node.left != null) queue.add(node.left); if (node.right != null) queue.add(node.right); } results.add(li); } return results; }The above implementation can also be achieved by recursive approach.
public static List<List<Integer>> levelOrderListsRec(TreeNode<Integer> root) { List<List<Integer>> results = new ArrayList<>(); helperListsRec(root, results, 0); return results; } private static void helperListsRec(TreeNode<Integer> root, List<List<Integer>> results, int level) { if (root == null) return; if (results.size() == level) { results.add(new ArrayList<>()); } results.get(level).add(root.val); helperListsRec(root.left, results, level + 1); helperListsRec(root.right, results, level + 1); }
Time complexity for different data structure
Other application case for Tree data structure
Binary Search Tree
reference
https://stackoverflow.com/a/23653021/15814147.
https://techvidvan.com/tutorials/java-abstract-data-type/#:~:text=What%20is%20an%20Abstract%20Data,of%20operations%20on%20that%20type.
Michael T. Goodrich. Data Structures and Algorithms in Java. 4th Edition. P264
https://java-questions.com/ds-time-complexity.html
