A project has already been created in local See docs here

Create a new repo on github. To avoid errors, do not initialize the new repository with README, license, or `.gitignore files. You can add these files after your project has been pushed to GitHub.
Open Terminal and change your working directory to your local folder
Initialize the local directory as a Git repository.
```
git init -b main
```
Add the files in your new local repository. This stages them for the first commit.
```
git add .
```
Commits the tracked changes and prepares them to be pushed to a remote repository. To remove this commit and modify the file, use git reset --soft HEAD~1 and commit and add the file again.

In Terminal, add the URL for the remote repository where your local repository will be pushed.

$ git remote add origin  <REMOTE_URL> 
# Sets the new remote
$ git remote -v
# Verifies the new remote URL

Push the changes in your local repository to GitHub.com.
```
git push origin main
```
origin is usually used for your own remote by convention.

2. Forking workflow

For working in the open source community or collaborating on your own projects

Resources

https://www.atlassian.com/git/tutorials/comparing-workflows/forking-workflow
https://gist.github.com/Chaser324/ce0505fbed06b947d962

Fork 'official' repo to your own remote github
Clone the forked repo from remote to your local system by git clone <url>

Origin is used for your personal remote forked repo by default while running git clone.
Add a remote for the 'official' repo
```
git remote add upstream <url>
```
Upstream is used for the official repository by convention.
Working in a branch: making & pushing changes
- Create a new branch for workflow git checkout -b new-branch
- Checkout to an existing branch git checkout some-branch
- keep your fork up to date to the latest 'official' repo git pull (upstream main)
Making a pull request
- push changes to my own remote repo that is accessible to others git push origin my-branch
- Cleaning work is probably needed before pull request.
  - Rebase your development branch to avoid conflict when new commits have been made to the upstream main branch.
```
git checkout my-branch
git rebase my-main
```
  - Squash several small commits to a more compact one by git rebase -i my-main
  More about git rebase can be found here.
- Create a "pull request" on github to let project maintainers know and then merge to upstream main.

3. Start from the beginning

Notes from Advanced Git Tutorial | Google IT Automation with Python

Git is a visual control system (VCS), which can save code, configrations, histories, etc.

After installing git, the first thing to do is to tell Git who you are by execute command line git config --global "me@email.com"

Add new project and repo

$ mkdir project
$ cd project

# Create a new repo in local
$ git init

Stage changes and commit

$ git status
$ git add .
$ git commit -m "comments"

# A shortcut to stage any changes to tracked files and commit them in one step 
# only for small changes
$ git commit -a -m"message"

Show changes in commit

# to show change logs
$ git log

# to show changes with details
$ git diff -u
# or 
$ git log -p

# shows only unstaged changes by default
$ git diff
# show changes staged but not commited
$ git diff --stanged

# review changes before staging them
git add -p

Remove or rename the file in the repo

# remove files from repo, stop the file from being tracked by git
$ git rm FILENAME

# check out the files in the directory/repo
$ ls -l
$ ls -al

# rename the file
$ git rename new_name old_name

# create .gitigore in root repo
$ touch .gitignore
# add files into .gitignore
$ echo .idea > .gitignore

Undo changes before committing
- Change the file back to previous state has not been staged: git checkout filename
- Change the file has been staged but not commit, counterpart to git add: git reset HEAD filename
Amend commit
- Overwrite previous commit (only works for local repo, not for remote repo): git commit --amend

Rollbacks

$ git revert HEAD // HEAD is regarded as a point to a snapshot
$ git revert commit_id

# identify a commit by commit_id
$ git log -p -2

Branch - a pointer to a particular commit

default branch - main (or master in old github)

# check up the current branch 
$ git branch

# create a new branch
$ git branch new_branch

# check out the latest snapshot for both files in this branch
$ git checkout new_branch

# create a new branch and switch to it
$ git checkout -b another_branch

# delete the branch
$ git branch -d old_branch

# merge a branch to another
$ git merge another_branch

merge conflict

git log --graph --oneline

git merge -abort - stop merging and back to previous status

4. How to reset and go back to your previous commit

First to check out the history change logs and find out which version I want to return back by commit_id: git lg
Then go to the log that I want to go by git reset commit_id

Be cautious of using git reset -hard commit_id
Lastly, add, commit, and push. If there is a new commit message after git reset operation, it will combine the last few commits that you do not want into a single commit.

Java

Java fundamentals

Exceptions

In Java, an exception is an event that disrupts the normal flow of the program ¹.

Many methods in Java to read and write files require that exceptions are handled. There are two main approaches: lbyl (look at before you leap) and eafp (easy to ask for forgiveness than permission).

Look at before you leap

In the following code, we check if the arguements are valid before operation.
```
private static int divideLBYL(int x, int y) {
    if (y != 0) return x / y;
    else return 0;
}
```

Easy to ask forgiveness than permission

In this approach, we run the method first and catch the exception if any exception (exception handler).

private static int divideEAFP(int x, int y) {
    try {
        return x / y;
    } catch(ArithmetricException e) {
        return 0;
    }
}

Checked Exception vs. Unchecked Exception

The Exception Handling in Java is one of the powerful mechanism to handle the runtime errors so that the normal flow of the application can be maintained. The Exception class family in Java is depicted below:

There are basically three types of exceptions: Checked Exception, Unchecked Exception, and Error. Sometimes, Error can be considered as Unchecked Exception.

Checked Exceptions: All the subclasses of Exception class except for RuntimeException and its subclasses are checked exceptions. That is, if there is an checked exception in the code, the program won't be compiled if no exception handling.

public class CheckedVsUnchecked {
    public static void main (String[] args) {
        readFile("myFile.txt");
    }

    private static void readFile (String fileName) {
        // will throw a FileNotFoundException, that is checked exception
        FileReader file = new FileReader(fileName);
    }
}

The above code would not compile because fileName may not exist, which will throw a FileNotFoundException (unchecked expcetion). To handle unchecked exception, we can use either try-catch method or throws exception in the function signature ². The difference between throw within a method and throws in a method signature can be found in this article.

public class CheckedVsUnchecked {
    // it is important to throw an exception in main method as well
    // in order to catch the exception thrown by readFile method
    public static void main (String[] args) throws FileNotFoundException {
        readFile("myFile.txt");
    }

    private static void readFile (String fileName) throws FileNotFoundException {
        FileReader file = new FileReader(fileName);
    }
}

Unchekced Exception: The RuntimeException subclass of the Exception class and all its subclasses are unchecked exception. Runtime will not check this type of exception and the program will be compile but may fail. For example,

public class CheckedVsUnchecked {
    public static void main (String[] args) {
        String name = null;
        printLength(name);  // will throw NullPointerException even compiled.
    }

    private static void printLength (String myString) {
        System.out.println(myString.length());
    }
}

In this case, it is better to use try-catch method to handle this exception.

Call stack

When throwing an expcetion, Java automatically prints a stack trace, which is showing the call stack. Each thread of execution has its own call stack, and the thread is shown in the first line of the stack call.

try-catch(-finally)

A common way to handle exception is to throw a new exception with some information to indicate where might go wrong. For example,

private static int divide() {
    int x, y;
    try {
        x = getInt(); // a self-defined method that can get input from typing the keyboard.
        y = getInt();
        return x / y;   
    } catch (NoSuchElementException e) {
        throw new NoSuchElementException("no suitable input");
    } catch (ArithmetricException e) {
        throw new ArithmetricException("attempt to divide by zero");
    }   
}

Alternatively, we could catch multiple exception in the main methods, such as

private static void main (String[] args) {
    try {
        int result = divide();
    } catch (ArithmetricException | NoSuchElementException e) {  // it is not logical symbol or
        System.out.println(e.toString);
        System.out.println("Unable to excute, the computer shutting down");
    }
}

When Java code throws an exception, the runtime looks up the stack for a method that has a handler (like catch) that can process it. If it finds one, it passes the exception to it. If it doesn't, the program exists.

No matter whether an exception occur in try-block or not, finally will ALWAYS be excuted. For example,

// Java program to demonstrate control flow of try-catch-finally clause
// when exception occur in try block but not handled in catch block
class GFG {
    public static void main (String[] args) {  
        // array of size 4.
        int[] arr = new int[4];
         
        try {
            int i = arr[4];
            // this statement will never execute
            // as exception is raised by above statement
            System.out.println("Inside try block");
        }
        // not a appropriate handler so the following statement will also not execute
        catch(NullPointerException ex) {
            System.out.println("Exception has been caught");
        }
         
        finally { // will execute
            System.out.println("finally block executed");
        } 
        // rest program will not execute
        System.out.println("Outside try-catch-finally clause");
    }
}

However, if NullPointerException was replaced by ArrayIndexOutOfBoundsException, the correct exception, the statement in the catch will execute.

Even if there is a return in try block, the finally statement will also be excuted.

private static int printAnumber () {
    try {
        return 3;
    } 
    catch (Exception e) {
        return 4;
    }
    finally {
        return 5;
    }
    // output: 5, becauase the finally statement will override the above statement.
}

Read and Write File

If we want to make object persist, we need to write object into a file. See an example as below. Remember to close the file after writing. Failing to close streams can really cause problems such as resouce link leak and lcoked file.

Java Thread

What is thread?

In Computer Science, a thread of execution is the smallest sequence of programmed instructions that can be managed independently by a scheduler (a part of operating system). 线程是操作系统能够进行运算调度的最小单位。In most of cases, a thread is a component of a process. The multiple threads of a given process may be executed concurrently (via multithreading capabilities), sharing resources such as memory, while different processes do not share these resources ³. Below is an illustration of relationship between program, process, thread, scheduling, etc.

The following image shows two threads running on one process.

In Java, a thread is a thread of excution in a program, i.e., the direction or path that is taken while a program is being excuted. The thread class extends Object and implements Runnable ⁴. A thread enables multiple operations to take place within a single method. Each thread in the program often has its own program counter, stack, and local variables.

Creating a Thread

There are two ways to create a new thread of execution. One is to declare a class to be a subclass of Thread. This subclass should override the run method of class Thread. An instance of the subclass can then be allocated and started.

To execute a thread, we need to call the start() function instead of run. The purpose of start() is to create a seperate call stack for the thread. See an example below:

class ThreadTest extends Thread {
    @Override
    public void run(){
        try {
            System.out.println("Thread " 
                            + Thread.currentThread().getId()
                            + " is running" )
        } 
        catch (Exception e) {
            e.printStackTrace();
        }
        
    }

    public static void main (String[] args) {
        for (int i = 0; i < 8; i ++) {
            ThreadTest test = new ThreadTest();
            test.run();
        }
    }
}

output:
Thread 1 is running
Thread 1 is running
Thread 1 is running
Thread 1 is running
Thread 1 is running
Thread 1 is running
Thread 1 is running
Thread 1 is running

Here only Thread 1 is running because of calling run() method directly, and the same call stack is used for all new thread. But if we change test.run() to test.start(), then we will have an output like Thread 10 is running, in which the number is randomly allocated. ⁵

public class MultiThreads extends Thread {
    @Override
    public void run() {
        for (int i = 0; i < 5; i++) {
            System.out.println(i);
        }
        
        try {
            Thread.sleep(1000);
        } catch (InterruptedException e) {
            e.printStackTrace();
        }
    }
}

Extending Thread Class

reference

https://www.javatpoint.com/exception-handling-in-java

https://www.youtube.com/watch?v=bCPClyGsVhc

https://en.wikipedia.org/wiki/Thread_(computing)

⁴

https://docs.oracle.com/javase/7/docs/api/java/lang/Thread.html

⁵

https://www.geeksforgeeks.org/start-function-multithreading-java/

Database

Data Structure

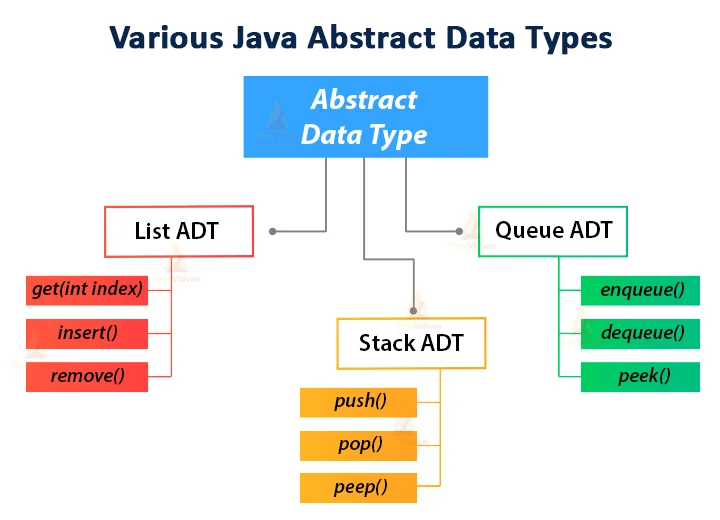
This document outlines the fundamental data structure in Java. The most commonly used data structures in Java include ArrayList, HashMap, Queue, Stack, and BST (Binary Search Tree). These data structures are clearly different but have some relationship. The following scheme exhibits the relationship of these data structures. Notice that some are Interface and some are Class.

Abstract Data Types (ADT) vs. interface

An abstract data type is a self-contained, user-defined type that bundles data with a set of related operations ¹. ADT can be classified as built-in and user-defined or as mutable or immutable ². For example, the List interface is a Java built-in ADT, which defines a data structure with set of methods to operate on but without providing detailed implementation.

My own understanding of ADT is that it is a general concept, and interfaces in Java is in-built ADT for convenience for users.

Implementing an ADT in Java involves two steps. The first step is the definition of a Java Application Programming Interface (API), for interface for short, which describes the names of the methods that the ADT supoorts and how they are to be declared and used. Secondly, we need to define exceptions for any error conditions that can arise during operations ³. Java libraty provides various ADTs such as List, Stack, Queue, Set, Map as inbuilt interfaces that we implement using various data structures.

Collecction

Java Collection interface provides a architecture to store and manipulate a group of objects. The java.util package contains all the classes and interfaces for the Collection framework. The Collection interface is implemented by all the classes in the framework, and it only declares the method that each collection will have.

List

List interface extends Collection interface, which stores a list type data structure in which we can store an ordered collection of objects, and can have duplicate values. List interface is implemented by the classes ArrayList, LinkedList, Vector and Stack.

ArrayList

uses a resieable array to store objects, built on top of array. The size, isEmpty, get, set and iterator operations run in constant time, while the add operation runs in amortized constant time. Other operations roughly run in linear time, and the constant factor is low compared to LinkedList.

LinkedList

a linear data structure that consists of nodes holding a data field and a reference to another node. It is a doubly-linked list implementing both List and Deque interface. Some commonly used methods and their corresponding run time complexity are listed below:

.add(): add element to the end of the list and run time is constant O(1).
.get(): get a specific element by traversing nodes one by one, and the worst run time is O(n).
.remove(element): remove an element with runtime O(n).

In general, except for add, other LInkedList operations run in linear time.

LinkedList implementing Deque interface, which is extended Queue interface, can retrive the first element and remove it from the list, i.e., linkedList.poll() and linkedList.pop(). Also, this linkedlist can also add an element to the head like a stack, i.e., linkedList.push(e).

Stack

a generic, linear data structure that represents a Last-In-First-Out(LIFO) collection of objects. It allows to push/pop element in a constant time. Stack is a direct class of Vector, which is a synchronized implementation. A more complete and consistent set of LIFO stack operations is provided by the Deque interface, which can be implemeneted by ArrayDeque, e.g., Deque<Integer> stack = new ArrayDeque<Integer>().

Stack is also an ADT, and it can be implemented using Array, ArrayDeque and a Generic LinkedList.

Queue

a interface following First-In-First-Our (FIFO) principle typically. Except for priority queue, it order elements according to a supplied comparator or the element's natural ordering. Regardless of ordering, .remove() or .poll()operations will remove an element from the head of the queue (so called dequeue), and new element will be inserted at the tail of the queue (enqueue).

Deque

a linear collection (interface) that supports element insertion and removal at both ends, for example, addFirst() and addLast(). The Deque interface extends Queue.

When Deque is used as a queue, the collection follows FIFO manner, in which The addLast() operation is equivalent to add() in queue method.
Deque can also be used as LIFO stacks, in which insertion and remove will be operated at the beginning of the deque. The pop and push operations will be equivalent to removeFirst and addFirst, respectively, in deque.

Unlike the List interface, the Deque interface does not provide support for indexed access to element.

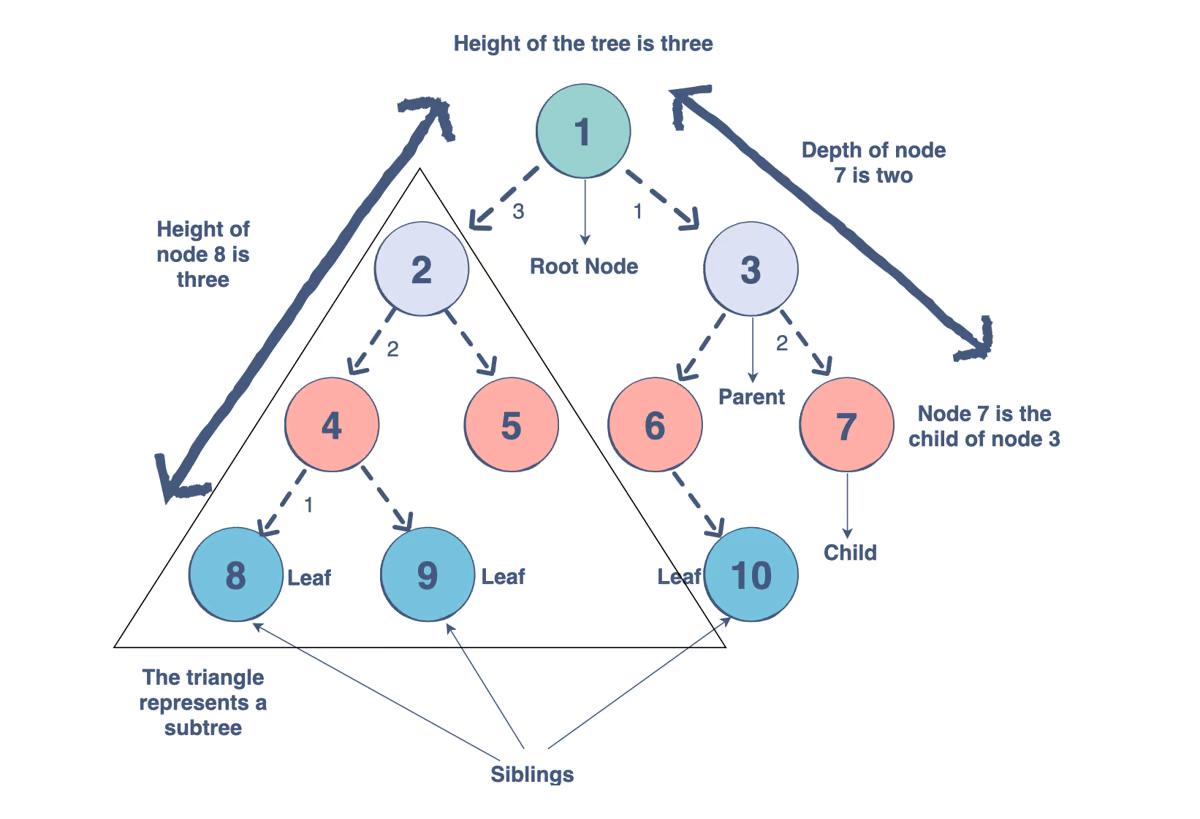
Tree

Tree structure and composition

Tree data structure

All the above mentioned data structures are linear, whereas Tree is a non-linear data structure. Tree is composed of a set of nodes, and each node store data of any types and a node pointing to its child nodes. The components and parameters of a tree is depicted below.

Types of trees: Binary Tree, Binary Search Tree (BST), Red-Black Tree (RBT), 2-3 Tree, 2-3-4 Tree and so on.

Applications with Tree

Storing hierarchy information, such file systems
Searching: Tree is more efficienct for searching than LinkedList
Inheritance: Trees are used for inheritance, XML parser, machine learning, and DNS, amongst many other things.
Indexing: Advanced types of trees, like B-Trees and B+ Trees, can be used for indexing a database.

and more ...

Treversal

There are two ways to traverse all nodes in a tree: Depth-First Traversal (DFT, 深度优先游历) and Breadth-First Traversal (BFT，深度优先游历).

Depth-First Traversal (DFT)

Usually implemented by stack if using iteration.

Preorder: visit node, go left, go right

An illustration of the reorder traversal using stack data structure is shown below.

The corresponding codes are:

public static ArrayList<Integer> preOrderTraversalStack(TreeNode<Integer> root) {
    // create a new ArrayList to store values
    ArrayList<Integer> li = new ArrayList<>();
    if (root == null) return li;
    // as it is DFT, uses stack
    Stack<TreeNode<Integer>> stack = new Stack<>();
    stack.push(root);
    while (!stack.isEmpty()) {
        TreeNode<Integer> node = stack.pop();
        // add node value to the list before push child nodes to the stack
        li.add(node.val);
        // due to FILO manner, push right child node in order to get the left child node
        if (node.right != null) stack.push(node.right);
        if (node.left != null) stack.push(node.left);
    }
    return li;
}

A more general method using Stack and Iteration:

public static List<Integer> preorderTraversalIter2(TreeNode<Integer> root) {
    List<Integer> list = new ArrayList<>();
    Stack<TreeNode<Integer>> stack = new Stack<>();
    TreeNode<Integer> node = root;
    while (node != null || !stack.empty()) {
        if (node != null) {
            stack.push(node);
            // add to the list once traverse on it
            list.add(node.val);
            node = node.left;
        } else {
            node = stack.pop();
            node = node.right;
        }
    }
    return list;
}

Using recursion to implement preorder traversal:

public static ArrayList<Integer> preOrderTraversalRec(TreeNode<Integer> root) {
    // create a new ArrayList to store values
    ArrayList<Integer> li = new ArrayList<>();
    if (root == null) return li;
    helperRecursion(root, li);
    return li;
}

private static void helperRecursion(TreeNode<Integer> root, ArrayList<Integer> li) {
    if (root == null) return;
    // Step 1: add node value to the list
    li.add(root.val);
    // Step 2: go left
    helperRecursion(root.left, li);
    // Step 3: go right
    helperRecursion(root.right, li);
}

Inorder: go left, visit node, go right

An illustration of the inorder traversal using stack data structure is shown below.

The corresponding implementation using stack is as follows:

public static List<Integer> inorderTraversalStack(TreeNode<Integer> root) {
    List<Integer> list = new ArrayList<>();
    Stack<TreeNode<Integer>> stack = new Stack<>();
    TreeNode<Integer> currNode = root;
    while(currNode!=null || !stack.empty()){
        // traverse along the left edge to the bottom
        if (currNode != null) {
            stack.push(currNode);
            currNode = currNode.left;
        } else {
            // pop each node from the stack and add value to the list
            currNode = stack.pop();
            list.add(currNode.val);
            // push the right child node if exists
            currNode = currNode.right;
        }
    }
    return list;
}

Recursion method:

public static ArrayList<Integer> inOrderTraversalRec(TreeNode<Integer> root) {
    ArrayList<Integer> li = new ArrayList<>();
    helperRecusion(root, li);
    return li;
}

private static void helperRecusion(TreeNode<Integer> root, ArrayList<Integer> li) {
    if (root == null) return;
    helperRecusion(root.left, li);
    li.add(root.val);
    helperRecusion(root.right, li);
}

Postorder: go left, go right, visit node

An illustration of the postorder traversal using stack data structure is shown below.

An example code for implementation of postorder traversal shows as follows

// method 1: Normal iteration
public List<Integer> postorderTraversalStack(TreeNode root) {
    Stack<TreeNode> stack = new Stack<>();
    LinkedList<Integer> li = new LinkedList<>();
    TreeNode node = root;
    while (node != null || !stack.isEmpty()) {
        while (node != null) {
            stack.push(node);
            node = node.left;
        }
        // unlike inorder traversal, here we only "peek" the node in the stack 
        // as we need to check if it has right child node
        node = stack.peek();
        // if it has, then traverse to the right child node
        if (node.right != null) {
            node = node.right;
        } else {
            // if it does not have, add this node value to the list
            node = stack.pop();
            li.add(node.val);
            // check if this node is a right child node
            // if it is, pop out the node and add the value to the list
            while (!stack.isEmpty() && node == stack.peek().right) {
                node = stack.pop();
                li.add(node.val);
            }
            node = null;
        }
    }
    return li;
}


// method 2: reverse preorder traversal
public static List<Integer> postorderTraversalStackRev(TreeNode<Integer> root) {
    Stack<TreeNode<Integer>> stack = new Stack<>();
    LinkedList<Integer> li = new LinkedList<>();
    TreeNode<Integer> node = root;
    while(node != null || !stack.isEmpty()) {
        if (node != null) {
            stack.push(node);
            // to reverse preorder traversal,
            // add the value of each node traversed to the head of the list
            li.addFirst(node.val);
            // until the right side bottom
            node = node.right;
        } else {
            node = stack.pop();
            node = node.left;
        }
    }
    return li;
}

Recursion method:

public static List<Integer> postorderTraversalRec(TreeNode<Integer> root) {
    List<Integer> li = new ArrayList<>();
    helperRecursion(root, li);
    return li;
}

private static void helperRecursion(TreeNode<Integer> root, List<Integer> li) {
    if (root == null) return;
    helperRecursion(root.left, li);
    helperRecursion(root.right, li);
    li.add(root.val);
}

Breadth-First Traversal (BFT)

Levelorder traversal: usually uses Queue to implement.

The following example returns a list of node values via BFT using iteractive method.

public static List<Integer> levelOrderStack(TreeNode<Integer> root) {
    List<Integer> li = new ArrayList<>();
    if (root == null) return li;
    Queue<TreeNode<Integer>> queue = new LinkedList<>();
    TreeNode<Integer> node = root;
    queue.add(node);
    while (!queue.isEmpty()) {
        node = queue.poll();
        li.add(node.val);
        if (node.left != null) queue.add(node.left);
        if (node.right != null) queue.add(node.right);
    }
    return li;
}

Here is another example to re the node values level by level by store the node values in list and append each list to a list of lists. The main difference from the above example is that we add an extra variable level to track which level of the node is.

public static List<List<Integer>> levelOrderLists(TreeNode<Integer> root) {
    List<List<Integer>> results = new ArrayList<>();
    // a queue to place each node traversed
    Queue<TreeNode<Integer>> queue = new LinkedList<>(); 
    if (root == null) return results;
    TreeNode<Integer> node = root;
    // add a variable to track level
    queue.add(node);
    while (!queue.isEmpty()) {
        List<Integer> li = new ArrayList<>();
        int level = queue.size();
        // add the value of the nodes in certain level to the corresponding list
        for (int i = 0; i < level; i++) {
            node = queue.remove();
            li.add(node.val);
            // if the node has child nodes, then add the child node to the queue and increase the level
            if (node.left != null) queue.add(node.left);
            if (node.right != null) queue.add(node.right);
        }
        results.add(li);
    }
    return results;
}

The above implementation can also be achieved by recursive approach.

public static List<List<Integer>> levelOrderListsRec(TreeNode<Integer> root) {
    List<List<Integer>> results = new ArrayList<>();
    helperListsRec(root, results, 0);
    return results;
}

private static void helperListsRec(TreeNode<Integer> root, List<List<Integer>> results, int level) {
    if (root == null) return;
    if (results.size() == level) {
        results.add(new ArrayList<>());
    }
    results.get(level).add(root.val);
    helperListsRec(root.left, results, level + 1);
    helperListsRec(root.right, results, level + 1);
}

Time complexity for different data structure

⁴

Other application case for Tree data structure

Binary Search Tree

reference

https://stackoverflow.com/a/23653021/15814147.

https://techvidvan.com/tutorials/java-abstract-data-type/#:~:text=What%20is%20an%20Abstract%20Data,of%20operations%20on%20that%20type.

Michael T. Goodrich. Data Structures and Algorithms in Java. 4th Edition. P264

⁴

https://java-questions.com/ds-time-complexity.html

Frontend

Vue3 and Javascript

How to create a dynamic router on a page

Vue-router Programmatic Navigation

const userId = '123'
router.push({ name: 'user', params: { userId } }) // -> /user/123
router.push({ path: `/user/${userId}` }) // -> /user/123
// This will NOT work
router.push({ path: '/user', params: { userId } }) // -> /user

In my case,

// In the component of Tombview
methods: {
    open: function (userId) {
      router.push({name: 'userTomb', params: {userId}})
    }

Dynamic Route Matching

// in the "router.js" file
const routes = [
    {name: 'userTomb', path: '/userTomb/:userId', component: userTomb}
]
// : refers to params

// In the new router page
const User = {
  template: '<div>User {{ $route.params.id }}</div>'
}

In my case,

{{ $route.params.userId }} // use this code to pass dynamic paramters.

When it is used in

{{ this.$route.params.userId }}

CSS Notes

Usefull link for CSS sstyle Note that you could not change html but only style

1 CSS rules

what this about

<style>
p {
    color: blue;
    font-size: 20px;
    width: 200px;
}

h1 {
    color: green;
    font-size: 36px;
    width: center;
}
</style>

p is a selector;

In the curly braces, there is a declaration, containing property ´´´color´´´and value ´´´blue´´´ zero or more declarations are allowed.

The collection of these CSS rules is what's called a stylesheet.

2 CSS selectors: Element, Class, and ID Selectors

2.1 element selector

 ... 

2.2 class selector

.blue {
    color: blue;
}

In html part: ...

2.3 id selector

Can only be used once in the HTML document.

#name {
    color:blue;
}

...

2.4 grouping selectors

div, .blue{
    color: blue;
}

3 Combining Selectors

3.1 Element with Class Selector

//Every p that has a class = "big"
p.big{
    font-size: 20 px
}

An example:

<p class="big"> ... </p> // font-size: 20px
<div class="big"> ... </div>

3.2 Child Selector

//every p that is a direct child of article
article > p {  
    color: blue;
}

<article><p>...</p></article> // only this content has blue text.
...
<p>...</p>
<article><div><p>...</p></div></article>

3.3 Descendant Selector

//every p that is inside (at any level) of article
article p {  
    color: blue;
}

<article><p>...</p></article> // Blue text
...
<p>...</p> // Unaffected
<article><div><p>...</p></div></article> // Blue text

3.4 Not Limited to element Selector

//every p that is inside (at any level) of element with class = colored""
.colored p {  
    color: blue;
}
//every element with class = "colored" that is a direct child of article element
article > .colored{  
    color: blue;
}

3.5 Summary

combining selectors

Element with class selector: selector.class
Child(direct) selector: selector>selector
Descendent selector: selector selector

4 Pseudo-Class Selector

:link :visited :hover :active :nth-child

Styling links is not exactly as straight forward as styling a regular element, and that's because links have states. And these states can be expressed using our pseudo-classes. An example:

header li {
    list-style: none
}
// visited means that HTML allows that after you click a particular link that a different style can be applied to that link than an unclicked link
// In our case, however, we don't want to differentiate between the two, so we'll style them both together.
a:link, a:visited {  // <a> tag defines a hyperlink, which is used to link from one page to another.
    text-decoration: none;
    background-color: green;
    border: 1px solid blue;
    display: block;  // <a> tag is an inline element. Here we change it to a block-level element.
    width: 200px;
    text-align: center;
    margin-bottom: 1px;
}
// An active is that state when the user actually clicks on the element but hasn't yet released his click. 
a:hover, a:active {
    background-color: red;
    color: purple;
}
// the nth child pseudo-selector allows you to target a particular element within a list.
header li:nth-child(3) {
    font-size: 24px;
}
// Set every odd member has a gray backgroud.
section div:nth-child(odd) {
    background-color: gray
}
// When the cursor hovers on the 4th member, the 4th member change the color to green.
section div:nth-child(4):hover {
    background-color: green;
    cursor: pointer;
}

5 Style placement

5.1 Head style `<style>...</style>`

Head styles are usually there override external ones.

5.2 Place style inline

Great for quick testing. ... // not recommended

5.3 External CSS stylesheet

Mostly-used one in real sites. <link rel="stylesheet" href="style.css"

6 Conflict resolution

6.1 Origin Precedence

when in conflict Simple rule: last declaration wins It is based on the principal that HTML is processed sequentially top to bottom.
when no conflict Sample rule: declarations merge

<!DOCTYPE html>
<html>
<head>
<meta charset="utf-8">
<title>Cascade of CSS</title>
<link rel="stylesheet" href="external.css"> 
<style>

p {
  color: maroon;
}

</style>
</head>
<body>
<h1>Origin Example</h1>
<p>The rule is simple: last declaration wins.</p> // color: maroon
<p style="color: black;">If there is no conflict, declarations merge into one rule.</p> // color: black
</body>
</html>

In external css stylesheet:

p {
  font-size: 130%;
  background-color: gray;
  color: white;
}

6.2 Inheritance

If you specify some CSS property on some element, all the children and grandchildren and so on and so on of that element will also inherit that property without you having to specify the property for each and every element.

6.3 Specificity

Most specific selector combination wines, which can be evaluated by score:

1	1	1	1
style="..."	id	class, pseudo-class, attribute	# of element

For example, div p {color: green;} score = 0002 div #myparag {color: blue;} score = 0101 div.big p {color: green;} score = 0012

<!DOCTYPE html>
<html>
<head>
<meta charset="utf-8">
<title>Inheritance in CSS</title>
<style>
header.navigation p { // score = 0012
  color: blue;
}
p.blurb { // score = 0011 
  color: red;
}
p {
  color: green !important;  // !important will override over specificity.
}
</style>
</head>
<body>
<header class="navigation">
  <p class="blurb">Lorem ipsum dolor sit amet, consectetur adipisicing elit. Vero soluta enim aut! Nihil nam obcaecati, fugiat sint sit libero voluptate eos incidunt odio neque cum, dignissimos aperiam, magnam nisi debitis.</p>
</header>
</body>
</html>

7 Styling Text

.style {
    font-family: Arial, Helvetica, sans-serif;
    color: #0000ff; // first '00': red; middle '00': green: last '00': blue
    font-style: italic;
    font-weight: bold;
    font-size: 24px;
    text-transform: capitalize;
    text-align: center;
    
}

body {
    font-size: 120%; // 120 % by default
}

body {
    font-size: 120%; // default font = 16px; current font = 19px;
}
<div style="font-size: 2em;"> 2em text // font size is two times the currect font - 38px
<div style="font-size: 2em;"> 4em text // font size = 76px
<div style="font-size: .5em;> 2em again! </div> // font size = 76px
</div> 
</div>

8 The Box Model

8.1 box-sizing

The box composes of margin, border, and padding. box-sizing: border-box; The width refers to the whole box, which is hihgly recommended. or box-sizing: content-box; The width refers to the content only, the default setting. However, it should be noted that the box-sizing property does not inherit. To solve the problem, we can use * selector, which can apply the CSS style inside to all the elements.

* {
    box-sizing:border-box;
}

8.2 Cumulative Margins

Horizontal margins are cumulative.
Vertical magins from two elements will collapse, and larger margin wins.

8.3 Content overflow

overflow: auto overflow: scroll overflow: hidden overflow: invisible

9 Background properties

<body>
<h1>The background property</h1>
<div id="bg">Wolala</div>
</body>

#bg {
    width: 500px;
    height: 500px;
    background-color: blue;
    background-image: url('cat.png') // Use an image as a background.
    background-repeat: no-repeat // repeat images or not.
    background-position: top right // set image position
    // or background: url('cat.png') no-repeat right center blue
}

10 Position Elements

10.1 by Floating

<!DOCTYPE html>
<html>
<head>
<meta charset="utf-8">
<title>Two Column Design</title>
<style>

* {
  box-sizing: border-box;
}

div {
  /*background-color: #00FFFF;*/
}
p {
  width: 50%;
  /*border: 1px solid black;*/
  float: left;  // float to the left of the last element.
  padding: 10px;
}

#p1 {
  /*background-color: #A52A2A;*/
}
#p2 {
  /*background-color: #DEB887;*/
}

section {
  clear: left;
}

</style>
</head>
<body>
<h1>Two Column Design</h1>

<div>
  <p id="p1">Lorem ipsum dolor sit amet, consectetur adipisicing elit. Quia distinctio aliquid cupiditate perferendis fuga, sit quasi alias vero sunt non, ratione earum dolores nihil! Consequuntur pariatur totam incidunt soluta expedita.</p>
  <p id="p2">Lorem ipsum dolor sit amet, consectetur adipisicing elit. Dicta beatae voluptatibus veniam placeat iure unde assumenda porro neque voluptate esse sit magnam facilis labore odit, provident a ea! Nulla, minima.Lorem ipsum dolor sit amet, consectetur adipisicing elit. Eius nemo vitae, cupiditate odio magnam reprehenderit esse eum reiciendis repellendus incidunt sequi! Autem, laudantium, accusamus. Doloribus tempora alias minima laborum, provident!</p>
  <section>This is regular content continuing after the the paragraph boxes.</section>
</div>


</body>
</html>

10.2 Relative and Absolute Element Positioning

Static positioning Normal document flow. Default for all, except html.
Relative Positioning Element is positioned relative to its position in normal document flow. Positioning CSS(offset) properties are: top, bottom, left, right. Html positioning is defaulted by relative
Absolute Positioning All offsets(top, bottom, left, right) are relative to the position of the nearst ancestor which has positioning set on it, other than static.

<!DOCTYPE html>
<html>
<head>
<meta charset="utf-8">
<title>Positioning Elements</title>
<style>
* {
  box-sizing: border-box;
  margin: 0;
  padding: 0;
}
h1 {
  margin-bottom: 15px;
}

div#container {
  background-color: #00FFFF;
  position: relative;
  top: 60px; // equivalent to 'from top'
}
p {
  width: 50px;
  height: 50px;
  border: 1px solid black;
  margin-bottom: 15px;
}
#p1 {
  background-color: #A52A2A;
  position: relative;
  top: 65px;
  left: 65px;
}
#p2 {
  background-color: #DEB887;
}
#p3 {
  background-color: #5F9EA0;
  position: absolute; // the absolute positioning needs a relative or an absolute parent or an ancestor.
  top: 0;
  left: 0;
}
#p4 {
  background-color: #FF7F50;
}

</style>
</head>
<body>
<h1>Positioning Elements</h1>

<div id="container">
  <p id="p1"></p>
  <p id="p2"></p>
  <p id="p3"></p>
  <p id="p4"></p>
</div>

</body>
</html>

11 Media Query Syntax

@media (max-width: 767px){ // media feature (resolves to true or false)
   p {
     color: blue;
   }

Media Query Common Features

@media(max-width: 800px) {...}

@media(orientation: portrait){...}

@media screen{...}

@media print{...}

Media Query Common Logical Operators

Devices with width within a range @media(min-width: 768px) and (max-width: 991px){...}
Comma is equivalent to OR @media(max-width: 768px), (min-width: 991px){...}

Media Query Common Approach

p {color: blue;} // base styles
@media(min-witdh: 1200px)
@media(min-width:992px) and (max-width:1199px) 
// Be sure that two sizes are not overlapped.

An example for how to use media queries

<!DOCTYPE html>
<html>
<head>
<meta charset="utf-8">
<title>Media Queries</title>
<style>

/********** Base styles **********/
h1 {
  margin-bottom: 15px;
}

p {
  border: 1px solid black;
  margin-bottom: 15px;
}
#p1 {
  background-color: #A52A2A;
  width: 300px;
  height: 300px;
}
#p2 {
  background-color: #DEB887;
  width: 50px;
  height: 50px;
}

/********** Large devices only **********/
@media (min-width: 1200px){
    #p1 {
        width: 80%; 
    // p1 at width 1200 pixels or wider will take 80% of our screen
    // when it is below 1200px, the p1 will go back to the original size.
    }
    #p2 {
        width: 150px;
        height: 150px;
    }
}

/********** Medium devices only **********/
@media (min-width: 992px) and (max-width: 1199px){
    #p1{
        width: 50%;
    }
    #p2 {
        width: 100px;
        height: 100px;
    }
}


</style>
</head>
<body>
<h1>Media Queries</h1>

<p id="p1"></p>
<p id="p2"></p>

</body>
</html>

Summary

Basic syntax of a media query ** @media(media feature) ** @media(media feature) logical operator (media feature)
Remember not to overlap breakpoints
Usually, you provide base styling. Then change or add to them in each media query.

12 Responsive Design

what is a responsive website? It is a site that's designed to adapt its layout to the viewing environment by using fluid, proportion-based grids, flexible images, and CSS3 media queries. 12 columns grid responsive layout Checkout here for an example.

12.1 Introduction to Bootstrap

Bootstrap is the most popular HTML, CSS and JS framework for developing responsive, mobile first projects on the web. [https://getbootstrap.com/] bootstrap depends on jQuery S0 jQuery also needs to be download.

12.2 Bootstrap grid system

<div class="container">  // your Bootstrap grid always has to be inside of a container wrapper or .container-fluid.
    <div class="row"> // The row class also creates a negative margin, to counteract the padding that the container class sets up.
        <div class="col-md-4">Col 1</div>
        ...
    </div>
</div>

12.2.1 Column class template

col-SIZE-SPAN

SIZE screen width range identifier columns will collapes (i.e., stack) below that width, unless another rule applies
SPAN How many columns element should span values: 1 through 12

<header class="container">  // your Bootstrap grid always has to be inside of a container wrapper.
    <nav class="row"> // The row class also creates a negative margin, to counteract the padding that the container class sets up.
        <div class="col-md-4">Col 1</div>
        ...
    </nav>
</header>

Python

Python Course (University of Michigan)

https://www.coursera.org/learn/python/home/welcome

I took the course in Feb. 2018 without any coding experience before. However, I do not feel I really get Python because of lack of practice/exercise.
My interests start moving to data analysis recently, and I realized Python is a powerful tool in the world of data analytics. Therefore, I tried to pick up the course again and hopefully I could know it better this time (after I finished CS50 last year)

— April 2021

Tips for writing Python (or any other code) Good names for variables Comments - documentation

Converting User Input

# convert floor number from Europe system to US system
inp=input('Europe floor?')
usf=int(inp) + 1
print('US floor', usf)

def abc():

$ \int x dx = \frac{x^2}{2} + C $

\[ \mu = \frac{1}{N} \sum_{i=0} x_i \\ \int_0^\infty \mathrm{e}^{-x},\mathrm{d}x \] https://en.wikibooks.org/wiki/LaTeX/Mathematics

Learning in a hard way

numpy.array

When creates a numpy.array a = numpy.array([1,2,3]). It is 1-dimensional if not specified. The shape of a can be checked out by a.shape, and it will output (3,).

The number of dimensions will be transformed from 1 to 2 by exploting

a1 = a.reshape(1,3), giving an output array([[1,2,3]])
a2 = a.reshape(3,1), giving an output

array([[1],
       [2],
       [3]])

array.sum

array.sum(axis=0): sum up along the column

a1.sum(axis=0)
#output: array([1, 2, 3])

a2.sum(axis=0)
#output: array([6])

array.sum(axis=1): sum up along the row

a1.sum(axis=1)
#output: array([6])

a2.sum(axis=1)
#output: array([1, 2, 3]) -> 1D array?

a.sum(axis=1) and a.sum(axis=0) give the same output array([6]) because of only one dimension.

Easy coding

´x = x + 1´ is qual to ´x += 1´

Virtualenv - virtual environment manager

venv for Python 3 or virtualen for Python 2

Installing packages using pip and virtual environments

Installing venv

This is how I did for my "Energy-data" project:

Copy the following code into "init_py.sh" file

#!/bin/bash
set -e

PYTHON_ENV_NAME=venv

pip3 install virtualenv

# or 'sudo pip3 install virtualenv'

virtualenv -p python3 $PYTHON_ENV_NAME

echo "source $(pwd)/$PYTHON_ENV_NAME/bin/activate" > .env

source $(pwd)/$PYTHON_ENV_NAME/bin/activate # activate the local python environment

pip3 install jupyter
pip3 install matplotlib
pip3 install pandas
pip3 install scipy
pip3 install seaborn
pip3 install graphviz
pip3 install scikit-learn

echo -e "\n"
echo "Please run \"$ source $PYTHON_ENV_NAME/bin/activate\" to switch to the python environment."
echo "Use \"$ deactivate\" anytime to deactivate the local python environment if you want to switch back to your default python."
echo "Or install autoenv as described on project readme file to make your life much easier."

Other easy ways to do

Video source from Corey Schafer

Text insruction

Statistics rewind

Probability - The Science of Uncertainty and Data (2021)

Use the course to re-build my statistics knowledge.

The course link

The Book

1 Sample Space and Probability

1.1 Sample space - A set of outcomes

discrete/finite example
continuous example

1.2 Probability Axioms

Nonnegativity $P(A) \geq 0 $
Normalization $ P( \Omega ) = 1 $, $\Omega $ is the entire sample space.
(finite) Additivity: A and B are disjoint, then the probability of their unions satisfies $P(A \cup B) = P(A) + P(B)$ (to be strengthened later)

1.2.1 Simple consequences of the axioms

For a sampe space consist of a finite number of disjointed events, \[ P({s_1, s_2, ...., s_n}) = P(s_1) + P(s_2) + ...... P(s_n) \]
$A \subset B$, then $P(A) \leq P(B)$
$P(A \cup B) = P(A) + P(B) - P(A \cap B)$
$P(A \cup B) \leq P(A) + P(B))$

1.3 Probability calculations

1.3.1 Uniform Probability Law

Discrete example

If the sample space consists of n possible outcomes which are equally likely (i.e., all single-element events have the same probability), \[ P(A) = \frac{\text{number of elements of A}}{n} \]
continuous example

probability = area

1.3.2 Discrete but infinite sample space

Sample space: {1, 2, 3 ....}

Given $P(n) = \frac{1}{2^n}$, n = 1, 2, 3....

As $ P(\Omega) = 1 $: $\frac{1}{2} + \frac{1}{4} + ....= \sum\limits_{n=1}^\infty \frac{1}{2^n} = \frac{1}{2}\sum\limits_{n=0}^\infty \frac{1}{2^n} = \frac{1}{2}\frac{1}{1-1/2} = 1$

1.3.3 Countable aditivity axiom

Additivity holds only for "countable" sequences of events

If $A_1, A_2, A_3 ...$ is an $\underline{\text{infinite sequence of disjoined events}}$,

\[ P(A_1 \cup A_2 ......) = P(A_1) + P(A_2) + ...... \]

1.4 Mathematical background

1.4.1 Sets - A collection of distinc elements

finite: e.g. {a, b, c, d}
infinite: the reals (R)
$ \Omega $ - the universal set
Ø - empty set

What are reals?

The reals include rational numbers (terminating decimals and non-terminating recurring decimals and irrational numbers (non-terminating non-reccuring decimals

1.4.2 Unions and intersection

1.4.3 De Morgans' Law

$ (S \cap T)^c = S^c \cup T^c $ and $ (S \cup T)^c = S^c \cap T^c $
$ (S^c \cap T^c)^c = S \cup T $

1.4.4 Other important mathematical backgrounds

Sequences and their limits

squence: an enumerated collection of objects
When does a sequence converge
- if $a_i \leq a_{i+1}$
  - the sequence "converge to $\infty$"
  - the sequence converge to some real number a
- if $|a_i - a| \leq b$, for $b_i \to 0$, then $a_i \to a$
Infinite series

series(infinte sums) vs. summation(finite sums)

$\sum\limits_{n=1}^\infty a_i = \lim\limits_{n\to\infty}\sum\limits_{i=1}^n a_i$
- $a_i \leq 0$: limit exists
- if term $a_i$ do not all have the same sign:
  
  a. limit does not exist
  
  b. limit may exist but be different if we sum in a different order
  
  c. Fact: limit exists and independent of order of summation if $\sum\limits_{n=1}^\infty |a_i| \leq \infty$
Geometric series (等比数列、等比级数)

$\sum\limits_{i=0}^\infty a^i = 1 + a + a^2 + ...... = \frac{1}{1-a} \text{ |a| < 1} $

1.4 Sets

1.4.1 Countable and uncountable infinite sets

Countable
- integers, pairs of positive integers, etc.
- rational numbers q (有理数), with 0 < q < 1
Uncountable - continuous numbers
- the interval [0, 1]
- the reals, the plane, etc.
How to prove the reals are uncountable - "Control's diagonalization argument"

Unit 2 Conditioning and independence

Refer to Section 1.3 - 1.5 in the textbook

2.1 Conditional and Bayes' Rules

2.1.1 The definition of conditional probability

P(A|B) = "probability of A, given that B occurred"

\[ P(A|B) = \frac{P(A \cap B )}{P(B)} \]

defined only when P(B) > 0

2.1.2 Conditional probabilities share properties of ordinary probabilities

$P(A|B) \geq 0$
$P(\Omega|B) = 1$
$P(B|B) < 0$
If $A \cap C = Ø$, then $P(A \cup C|B) = P(A|B) + P(C|B)$ also only applies to countable and finite sequence (countable additivity axioms).

2.1.3 Models base on conditional probabilities

1. The multiplication rule

\\(P(A \cap B) = P(B)P(A|B) = P(A)P(B|A)\\)

\\(P(A^c \cap B \cap C^c) = P(A^c \cap B) P(C^c|A^c \cap B) = P(A^c) P(B|A^c) P(C^c|A^c \cap B)\\)

\\(P(A_1 \cap A_2...\cap A_n) = P(A_1) \prod\limits_{i=2}^n P(A_i|A_1 \cap A_2...\cap A_i)\\)

2. Total probability theorem

3. Bayes' rules

2.2 Independence

2.2.1 Conditional independence

Independent of two events

Intuitive "definition": P(B|A) = P(B)
- Occurence of A provides no new information about B

Definition of independence:

$P(A \cap B) = P(A) \times P(B)$

whether two events disjoined or joined is not associated with independence

Independent of events complements

If A and B are independent, then A and $B^c$ are independent.

Independent of events complements

Conditioning may affect independence

2.2.2 Independence of a collection of events

Intuitive "definition": Information on some of the events does not change probabilities related to the remaining events
Definition: Events $A_1, A_2,....., A_n$ are called independent if:

$P(A_i \cap A_j \cap .... \cap A_m) = P(A_i)P(A_j)...P(A_m)$

Pairwise independence

n = 3:

$P(A_1 \cap A_2) = P(A_1)P(A_2)$

$P(A_1 \cap A_3) = P(A_1)P(A_3)$

$P(A_2 \cap A_3) = P(A_2)P(A_3)$

vs. 3-way indenpendence

$P(A_1 \cap A_2 \cap A_3) = P(A_1)P(A_2)P(A_3)$

Independence vs. pairwise independence

2.2.3 Reliability

Unit 3 Couting

3.1 Basic counting principle

r stages and $n_i$ choices at stage i give the total number of possible choices $ n_1 * n_2 * ....n_r $

3.2 Permutation

Permutation - number of ways of ordering n elements (repetition is prohibited)

\[n * (n-1) * (n-2) * ... * 2 * 1 = n!\]

Number of subsets of {1, 2, ...n} = $2^n$

3.3 Combinations

combinations $\binom{n}{k}$- number of k-element subsets of a given n-element set

How is combination equation derived?

Two ways of constructing an ordered sequence of k distinct items:
- choose the k items one at a time:
  
  \[ n (n-1) ... (n-k+1) = \frac{n!}{k!(n-k)!} \]
- choose k items, then order them:
  
  \[ \left( \begin{array}{c} n \\ k \end{array} \right)k! \]
There we have \[ \left( \begin{array}{c} n \\ k \end{array} \right) = \frac{n!}{k!(n-k)!} \]

3.3 Binominal coeffficient

Binominal coeffficient $\binom{n}{k}$ - Binomial probabilities

Toss coins n times and each toss is given independent, P(Head) = p

\[ P(\text{k heads}) = \binom{n}{k}p^k (1-p)^{n-k} \]

If asking P(k heads without ordered), then

\[ P(\text{k heads}) = p^k (1-p)^{n-k} \]

Therefore, $\binom{n}{k}$ is the number of k-head sequence

3.4 Partitions

multinomial coeffecient (number of partitions) =

\[ \frac{n!}{n_1! n_2! ... n_r!} \]

If r = 2, then $n_1 = k$ and $n_2 = n - k$. There is $\frac{n!}{n! (n-k)!}$ which is $\binom{n}{k}$

A simple example

4 Discrete random variables

4.1 Probability mass function (PMF)

Random variable(r.v.): a function from the sample space to the real numbers, notated as X.

PMF: probability distribution of X

\[ p_X(x) = P(X = x) = P({w \in \Omega, s.t. X(\omega) = x}) \]

4.2 Discrete Random variable examples

4.2.1 Bernoulli random variables

with parameter $p \in [0,1]$

\[ p_X(x) = \begin{cases} 1, p(x) = p \\ 0, p(x) = 1 - p \end{cases} \]

Models a trial that results in either success/failure, Heads/Tails, etc.
Indicator random variables of an event A, $I_A$ iff A occurs

4.2.2 Uniform random variables

with paramters a,b

Experiment: pick one of a, a+1 .... b at a random; all equally likely
Sample space; {a, a + 1, .... b}
Random variables X: $X(\omega) = \omega$

4.2.3 Binomial random variables

with parameters: pasitive integer $n; p \in [0,1]$

Experiment: n independent toses of a coin with P(Heads) = p
Sample space: set of sequences of H and T of length n
Random variables X: number of Heads observed
Model of: number of successes in a given number of independent trials

\[ p_X(k) = \left(\begin{array}{c} n \\ k \end{array} \right)p^k(1-p)^{n-k}, k = 0, 1 ..., n \]

4.2.4 Geometric random variables

with parameter p: 0 < p ≤ 1

Experiment: infinitely many independent tosses of a coin: P(Heads) = p
Random variable X: number of tosses until the first Heads
Model of waiting times; number of tirals until a success

\[ p_X(k) = P(X = k) = P(T...TH) =(1-p)^{k-1}p, k = 1,2,3...
\]

4.3 Expectation/mean of a random variable

Definition:

\[ E[X] = \sum\limits_{x} xp_X(x) \]
Interpretation: average in large number of independet repetitions of the experiment
Elementary properties
- If X ≥ 0, then E(X) ≥ 0
- If a ≤ X ≤ b, then a ≤ E[X] ≤ b
- If c is a constant, E[c] = c
- The expected value rule:
  
  \[ E[Y] = \sum\limits_y yp_Y(y) = E[g(X)] = \sum\limits_x g(x)p_X(x)
  \]
- Linearity of expectation: $E[aX+b] = aE[X] + b$

4.4 Variance - a measure of the spread of a PMF

4.4.1 Definition of variance:

\[ var(X) = E[(X - \mu)^2] = \sum\limits_x (x - \mu)^2 p_X(x) \]

standard deviation: $\sigma_X = \sqrt{var(X)}$

4.4.2 Properties of the variance

Notation: $\mu = E[X] $
$var(aX + b) = a^2var(X)$
A useful formula:

\[ var(X) = E(X^2) - (E[X])^2
\]

Summary of Expectation and Variance of Discrete Random Variables

Random Variables	Formula	E(X)	var(X)
Bernoulli (p)	$p_X(x) = \begin{cases} 1, p(x) = p \\ 0, p(x) = 1 - p \end{cases} $	$p$	$p(1-p)$
Uniform (a,b)	$p_X(x) = \frac{1}{b-a}, a ≤ x ≤ b$	$\frac{a+b}{2}$	$\frac{1}{12}(b-a)(b-a-2)$
Binomial $p \in [0,1]$	$p_X(k) = \left(\begin{array}{c} n \\ k \end{array} \right)p^k(1-p)^{n-k}, k = 0, 1 ..., n$	$ np $	$np(1-p)$
Geometric $0 < p ≤ 1$	$p_X(k) = (1-p)^{k-1}p, k = 1,2,3.... $	$\frac{1}{p}$

4.5 Conditional PMF and expectation, given an event

4.5.1 Conditional PMFs

$p_{X|A}(x|A) = P(X = x|A)$, given A = {Y = y}

\[ p_{X|Y}(x|y) = \frac{p_{X,Y}(x,y)}{p_Y(y)}
\]

4.5.2 Conditional PMFs involing more than two random variables

$p_{X|Y,Z}(x|y,z) = P(X = x|Y = y, Z = z) = \frac{P(X=x,Y=y,Z=z)}{P(Y=y, Z=z)} = \frac{P_{X,Y,Z}(x,y,z)}{P_{Y,Z}(y,z)} $
Multiplication rules: $p_{X,Y,Z}(x,y,z) = p_X(x)p_{Y|X}(y|x)p_{Z|X,Y}(z|x,y) $
Total probability and expectation theorems

$p_X(x) = P(A_1)p_{X|A_1}(x) + ... + P(A_n)p_{X|A_n}(x) \implies p_X(x) = \sum\limits_y p_Y(y)p_{X|Y}(x|y)$

$E[X] = P(A_1)E[X|A_1] + ... + P(A_n)E[X|A_n] \implies E[X] = \sum\limits_y p_Y(y) E[X|Y = y]$

4.6 Multiple random variables and joint PMFs

4.6.1 Joint PMF

\[ p_{X,Y}(x,y) = P(X = x, Y =y) \]

$\sum\limits_x \sum\limits_y p_{X,Y}(x,y) = 1$
Marginal PMFs: $p_X(x) = \sum\limits_y p_{X,Y}(x,y)$

$p_Y(y) = \sum\limits_x p_{X,Y}(x,y)$

4.6.2 Functions of multiple random variables

$Z = g(X,Y)$

PMF: $p_Z(z) = P(Z=z) =P(g(X,Y) = z) $
Expected value rules: $E[g(X,Y)] = \sum\limits_x \sum\limits_y g(x,y) p_{X,Y}(x,y)$
Linearity of expectations
- $E[aX + b] = aE[X] + b$
- $E[X + Y] = E[X] + E[Y]$

4.6.3 Independence of multiple random variables

$P(X = x and Y = y) = P(X = x) \times P(Y = y), for all x, y $
$P_{X|Y}(x|y) = P_X(x)$ and $P_{Y|X}(y|x) = P_Y(y)$
Independence and expectations
- In general, $E[g(X,Y)] \neq g(E[X], E[Y])$
- If X, Y are independent: $E[XY] = E[X]E[Y]$
  
  g(X) and h(Y) are also independent: $E[g(X)h(Y)] = E[g(X)]E[h(Y)]$
Independence and variances
- Always true: $var(aX) = a^2var(X)$ and $var(X+a) = var(X)$
- In general: $var(X+Y) \neq var(X) + var(Y)$
- If X, Y are independent, $var(X,Y) = var(X) + var(Y)$

5 Continuous random variables

5.1 Probability density function (PDFs)

5.1.1 Definition

PDFs are not probabilities. Their units are probability per unit length.

Contiunous random variables: a random variable is continuous if it can be described by a PDF.

$P(X = a) = 0$
$f_X(x) \geq 0$
$\int_{-\infty}^{+\infty}f(x)dx = 1$

Expectation/Mean

Expection/mean of a continuous random variable: average in large number of independent repetitions of the experiment

\[ E[X] = \int_{-\infty}^{+\infty}xf_X(x)dx \]

Properties of expectations

if X ≥ 0, then $E[X] ≥ 0$
if a ≤ X ≤ b, then $a ≤ E[X] ≤ b$
Expected value rule: $E[g(X)] = \sum\limits_{x} g(x) f_X(x) dx $
Linearity: $E[aX + b] = aE(X) + b$

Variance

According to the definition of variance: $var(X) = E[(X - \mu)^2] $

\[ var(X) = \int_{-\infty}^{+\infty} (x - \mu)^2 f_X(x) dx \]

Standard deviation = $\sigma_X = \sqrt{var(X)} $
$var(aX + b) = a^2 var(X)$
$var(X) = E[X^2] - (E[X])^2$

Summary of Expectation and Variance of continuous random variables

Random Variables	Formula	E(X)	var(X)
Uniform	$f(x) = \frac{1}{b-a}, a ≤ x ≤ b$	$\frac{a+b}{2}$	$\frac{(b-a)^2}{12}$
Exponential $ \lambda > 0 $	$f(x) = \begin{cases} \lambda e^{-\lambda x}, x ≥ 0 \\ 0, x < 0 \end{cases}$	$\frac{1}{\lambda}$	$\frac{1}{\lambda^2}$

5.1.2 Cumulative distribution functions (CDF)

CDF defination: $F_X(x) = P(X ≤ x )$

Non-decreasing
$F_X(x)$ tends to 1, as $x \to \infty$
$F_X(x)$ tends to 0, as $x \to - \infty$

5.1.3 Normal(Gaussian) random variables

Standard normal(Gaussian) random variables

Stardard normal $N(0,1): f_X(x) = \frac{1}{\sqrt{2\pi}} e^{-x^2/2} $
- $E[X] = 0$
- $var(X) = 1$
General normal(Gaussian) random variables

General normal $N(\mu,\sigma^2): f_X(x) = \frac{1}{\sigma\sqrt{2\pi}} e^{-(x-\mu)^2/2\sigma^2}, \sigma > 0 $
- $E[X] = \mu $
- $ var(X) = \sigma^2 $
```
 \$ \sigma^2 \to small\$, the shape of normal distribution becomes more narrow.
```
Linear functions of a normal random variable
- Let $Y = aX + b, X \sim N(\mu, \sigma^2)$
  
  $E[Y] = a\mu + b$
  
  $Var(Y) = a^2 \sigma^2 $
- Fact: $Y \sim N(a\mu + b, a^2 \sigma^2)$
- Special case: a = 0. There is Y = b, $N(b, 0)$

5.1.4 Calculation of normal probabilities

Standard normal tables

$\Phi(y) = F_Y(y) = P(Y \leq y)$ which can be find in the table, where y ≥ 0.
Standardizing a random variable

$X \sim N(\mu, \sigma^2), \sigma^2 > 0 $

$Y = \frac{X - \mu}{\sigma}$

5.2 Conditioning on an event: multiple continuous r.v.'s

\[ P( X \in B|A) = \int_B f_{X|A}(x)dx \]

5.2.1 Conditional PDf of X, given that $X \in A $

\[ f_{X|X \in A}(x) = \begin{cases} 0, if x \notin A \\ \frac{f_X(x)}{P(A)}, if x \in A \end{cases} \]

5.2.2 Conditional expectation of X, given an event

5.2.3 Memorylessness of the exponential PDF

5.2.4 Total probability and expectation theorems

Probability theorem:

\[ P(B) = P(A_1)P(B|A_1) + \dotsb + P(A_n)P(B|A_n) \]

For the discrete random variable:

\[ p_X(x) = P(A_1)p_{X|A_1}(x) + \dotsb + P(A_n)p_{X|A_n}(x) \]

For CDF:

\[ F_X(x) = P(X \leq x) = P(A_1)P(X \leq x | A_1) + \dotsb + P(A_n)P(X \leq x | A_n) \\= P(A_1)F_{X|A_1}(x) + \dotsb + P(A_n)F_{X|A_n}(x) \]

For PDF, the derivative of CDF:

\[ f_X(x) = P(X \leq x) = P(A_1)f_{X|A_1}(x) + \dotsb + P(A_n)f_{X|A_n}(x) \]

Integral above equation, we will obtain the expectation equation:

\[ \int xf_X(x)dx = P(A_1) \int xf_{X|A_1}(x)dx + \dotsb + P(A_n) \int xf_{X|A_n}(x)dx \]

\[ E[X] = P(A_1)E[X|A_1] + \dotsb + P(A_n)E[X|A_n]
\]

5.3 Mixed random varibles

5.3.1 Mixed distirbutions

\[ X = \begin{cases} Y, \text{with probability } p \text{ (Y discrete)}\\ Z, \text{with probability } 1-p \text{ (Z continuous)} \end{cases}
\]

do not have PDF or PMF but can be defined with CDF and expectation

\[ F_X(x) = p P(Y \leq x) + (1-p) P(Z \leq x) \\ =pF_Y(x) + (1-p)F_Z(x) \\ = E[X] = p E[Y] + (1-p) E[Z] \]

5.3.2 Joint PDFs

Joint PDFs are denoted as $f_{X,Y}(x,y)$: probaility per unit area

When X = Y, equal to a line, meaning X and Y are not joint PDFs.

5.3.3 From the joint to the marginal

5.3.4 Joint CDF

\[ F_{X,Y}(x,y) = P(X \leq x, Y \leq y) = \int\limits_{-\infty}^{y} \int\limits_{-\infty}^{x} f_{x,y}(s,t)dsdt \]

5.4 Conditioning on a random variable and Bayers rule

5.4.1 Conditional PDFs, given another r.v.

$f_{X|Y}(x|y) = \frac{f_{X,Y}(x,y)}{f_Y(y)}$, if $f_y(y) > 0$
- $f_{X|Y}(x|y) \geq 0$
- Think of value of Y as fixed at some y shape of $f_{X|Y}(\cdot|y)$: slice of the joint
- multiplication rule:
  
  \[ f_{X|Y}(x,y) = f_Y(y) \cdot f_{X|Y}(x|y)
  \]
$P(X \in A | Y = y) = \int_A f_{X|Y}(x/y)dx$

5.4.2 Total probability and expectation theorems

Anolog to the PMFs of discrete randome varable $p_X(x) = \sum\limits_y p_Y(y)p_{X|Y}(x|y)$

For continuous r.v., there is

\[ f_X(x) = \sum_{-\infty}^{\infty} f_Y(y)f_{X|Y}(x|y)dy
\]
Anolog to the Expectation of discrete randome varable $E[X|Y=y] = \sum\limits_x x p_{X|Y}(x|y)$

For continuous r.v., there is

\[ E[X|Y=y] = \int_{-\infty}^{\infty} xf_{X|Y}(x|y)dx
\]
Anolog to the discrete randome varable $E[X] = \sum\limits_y p_Y(y) E[X|Y=y]$

For continuous r.v., there is

\[
E[X] = \int_{-\infty}^{\infty} f_Y(y)E[X|Y=y]dy
\\ = \int_{-\infty}^{\infty} xf_X(x)dx
\]
Expected value rule

\[ E[g(X)|Y=y] = \int_{-\infty}^{\infty} g(x)f_{X|Y}(x|y)dx
\]

5.4.3 Independence

\[ f_{X,Y}(x,y) = f_X(x)f_Y(y), for all x and y
\]

$f_{X,Y}(x,y) = f_X(x)$, for all y with $f_Y(y) > 0$ and all x
If X, Y are independent:

\[ E[XY] = E[X]E[Y] \\ var(X + Y) = var(X) + var(Y) \]

g(X) and h(Y) are also independent: $E[g(X)h(Y)] = E[g(X)] \cdot E[h(Y)]$

5.4.4 The Bayes rule --- a theme with variations

For discrete r.v.,
- $p_{X|Y}(x|y) = \frac{p_X(x) p_{Y|X}(y|x)}{p_Y(y)}$
- $p_Y(y) = \sum\limits_{x'} p_X(x')p_{Y|X}(y|x')$
For continuous r.v.,
- $f_{X|Y}(x|y) = \frac{f_X(x) f_{Y|X}(y|x)}{_Y(y)}$
- $p_Y(y) = \int\limits f_X(x')f_{Y|X}(y|x')$
One discrete and one continuous r.v.

Unit 6 Further topics on random variables

6.1 Derived distributions

6.1.1 A linear function $Y = aX + b$

Discrete r.v.

$ p_Y(y) = p_X(\frac{y-b}{a}) $
Continuous r.v.

$ f_Y(y) = \frac{1}{|a|}f_X(\frac{y-b}{a}) $
- A linear function of normal r.v. is normal
  
  If $X \sim N(\mu, \sigma^2)$, then $aX + b \sim N(a\mu + b, a^2\sigma^2)$

6.1.2 A general function $g(X)$ of a continuous r.v.

Two-step procedure:

Find the CDF of Y: $F_Y(y) = P(Y \leq y) = P(g(x) \leq y)$ and the valid range of y
Differentiate: $f_Y(y) = \frac{dF_Y(y)}{dy}$

A general formula for the PDF of $Y = g(X)$ when g is monotomic

\[ f_Y(y) = f_X(h(y))\left|\frac{dh(y)}{dy}\right|
\]

$x = h(y)$ is the inverse function of $y = g(x)$
A nonmonotonic example $Y = X^2$
- the discrete case: $p_Y(y) = p_X(\sqrt{y}) + p_X(-\sqrt{y})$
- the continuous case: $f_Y(y) = f_X(\sqrt{y})\frac{1}{2\sqrt{y}} + p_X(-\sqrt{y})\frac{1}{2\sqrt{y}}$
A function of multiple r.v.'s: $Z = g(X,Y)$

6.2 Sums of independent vadom variables

6.2.1 The distribution of $X + Y$: the discrete case

Z = X + Y; X,Y independent, discrete known PMFs

\[ p_Z(z) = \sum\limits_x p_X(x)p_Y(z-x)
\]

Dsicrete convoltion mechanics

Flip the PMF of Y and put it underneath the PMF of X
Shift the flipped PMF by z
Cross-multiply and add

6.2.2 The distribution of $X + Y$: the continous case

Z = X + Y; X,Y independent, continuous known PDFs

\[ f_Z(z) = \int\limits_x f_X(x)f_Y(z-x)dx
\]

conditional on $X = x$:

\[ f_{Z|x}(z|x) = f_Y(z-x)
\]

which can then be used to calculate Joint PDF of Z and X and marginal PDF of Z.
Same mechanics as in discrete case

6.2.3 The sum of independent normal r.v.'s

$X \sim N(\mu_x, \sigma_x^2), Y \sim N(\mu_y, \sigma_y^2$ Independent

$Z = X + Y: \sim N(N(\mu_x + \mu_y, \sigma_x^2 + \sigma_y^2))$

The sum of finitely many independent normals is normal

6.3 Covariance (协方差)

6.3.1 Definition

\[ cov(X,Y) = E[(X - E[X]) \cdot (Y - E(Y))]
\]

If $X,Y$ independent: $cov(X,Y) = 0 $

convers is not true!

6.3.2 Covariance properties

$cov(X,X) = var(X) = E[X^2] - (E[X])^2$
$cov(aX+b,Y) = a \cdot cov(X,Y)$
$cov(X,Y+Z) = cov(X,Y) + cov(X,Z)$

Practical covariance formula:

\[ cov(X,Y) = E[XY] - E[X]E[Y] \]

6.3.3 The variance of a sum of random variables

two r.v.s

\[ var(X_1 + X_2) = var(X_1) + var(X_2) + 2cov(X_1,X_2)
\]

X,Y indepedent, then $var(X_1 + X_2) = var(X_1) + var(X_2)$
multiple r.v.s

\[ var(X_1 + \dots + X_n) = \sum\limits_{i=1}^nvar(X_i) + \sum\limits_{(i,j):i \neq j}^n cov(X_i,X_j)
\]

$\sum\limits_{(i,j):i \neq j}^n $ contains $(n^2 - n)$ terms

6.4 The correlation coefficient

\[ \rho(X,Y) = E\left[\frac{(X - E[X])}{\sigma_X} \cdot \frac{(Y - E[Y])}{\sigma_Y}\right] = \frac{cov(X,Y)}{\sigma_X \sigma_Y} \]

6.4.1 Interpretation of correlation coeffecient

Dimensionless version of covariance
Measure of the defree of "association" between X and Y
Association does not imply causation or influence
Correlation often refleces underlying, common, hidden factor

6.4.2 Key properties of the correlation coeffecient

$-1 \leq \rho \leq 1$
Independent $\implies \rho = 0$ "uncorrelated" (converse is not true)
$|\rho| = 1 \Leftrightarrow$ linearly related
$cov(aX+b, Y) = a \cdot cov(X,Y) \implies \rho(aX+b,Y) = sigma(a)\rho(X,Y)$

6.5 Conditional expectation and variance as a random variable

6.5.1 Conditional expecation

Definition: $g(Y)$ is the random variable that takes the value $E[X|Y=y]$, if $Y$ happens to take the value $y$.

\[ E[X|Y] = g(Y)
\]

Law of iterated expectations

\[ E[E[X|Y]] = E[g(Y)] = E[X]
\]

6.5.2 Conditional variance

Variance fundamentals

\[ var(X) = E[(X - E[X])^2] \\ var(X|Y=y) = E[(X - E[X|Y=y])^2|Y=y] \]

var(X|Y) is the r.v. that takes the value var(X|Y=y), when Y=y

Law of total variance

\[ var(X) = E[var(X|Y)] + var(E[X|Y])
\]

var(X) = (average variability within sections) + (variability between sections)

6.6 Sum a random number of indepedent r.v.'s

Example of shopping

N: number of stores visited (N is a nonnegative integer r.v.)
$X_i$: money spent in store i
- $X_i$ independent, identically distributed
- independent of N
Let $Y = X_1 + \dots + X_N$

6.6.1 Expecatation of the sum

Based on the Law of iterated expectations:

\[ E[Y] = E[E[Y|N]] = E[N \cdot E[X]] = \cdot E[X]E[N]
\]

6.6.2 Variance of the sum

Based on the Law of total variance: $var(Y) = E[var(Y|N)] + var(E[Y|N])$:

\[ var(Y) = E[N]var(X) + (E[X])^2var(N) \]

Unit 7 Bayesian inferences

7.1 Introduction to Bayesian inference

7.1.1 Basic concepts

Model building versus inferring unobserved variables

\[X = aS + W\]

S: signal; W: noise; a: medium (image a black box where S goes through and output X with W as noise)
- Model building: known signal S, observe X -> infer a
- Variable estimation: known a, observe X -> infer S
Hypothesis testing vs. estimation
- Hypothesis testing
  - unknown takes one of few possible values
  - aim at small probability of incorrect decision
- Estimation
  - numerical unknown(s)
  - aim at an estimate that is "close" to the true but unknown value

7.1.2 The Bayescian inference framework

Unknown $\Theta$ - treated as a random variable prior distribution: $p_{\Theta}$ or $f_{\Theta}$
Observation $X$ - observation model $p_{X|\Theta}$ or $f_{X|\Theta}$
Use appropriate version of the Bayes rule to find $p_{X|\Theta}(\cdot | X = x)$ or $f_{X|\Theta} (\cdot| X = x)$

The output of Bayesian inference - posterior distribution
- Maximum a posterior probability (MAP):
  
  $p_{\Theta|X}(\theta^*|x) = \max\limits_{\theta} p_{\Theta|X}(\theta|x)$
  
  $f_{\Theta|X}(\theta^*|x) = \max\limits_{\theta} f_{\Theta|X}(\theta|x)$
- Conditional expectation: $E[\Theta|X = x]$ Least Mean Square (LMS)
- estimate: $\hat{\theta} = g(x)$ (number)
- estimator: $\hat{\Theta} = g(X)$ (random variable)

7.1.3 Four cases

Discrete $\Theta$, discrete X
- values of $\Theta$: alternative hypotheses
\[ p_{\Theta|X}(\theta|x) = \frac{p_{\Theta}(\theta)p_{X|\Theta}(x|\theta)}{p_X(x)}
\]

\[ p_X(x) = \sum\limits_{\theta'}p_{\Theta}(\theta')p_{X|\Theta}(x|\theta') \]
- conditional prob of error: Smallest under the MAP rule
```
 \\[
     P(\hat{\theta} \neq \Theta|X = x)
 \\] 
```
- overal probability of error:
```
 \\[
     P(\hat{\Theta} \neq \Theta) = \sum\limits_{x} P(\hat{\Theta} \neq \Theta|X = x)p_X(x) = \sum\limits_{\theta}P(\hat{\Theta} \neq \Theta|\Theta = \theta)p_{\Theta}(\theta)
 \\] 
```
Discrete $\Theta$, Continuous X

\[ p_{\Theta|X}(\theta|x) = \frac{p_{\Theta}(\theta)f_{X|\Theta}(x|\theta)}{f_X(x)}
\]

\[ f_X(x) = \sum\limits_{\theta'}p_{\Theta}(\theta')f_{x|\Theta}(x|\theta') \]
- the same equation for conditional prob. of error
- overall probability of error
  
  \[ P(\hat{\Theta} \neq \Theta) = \int\limits_{x} P(\hat{\Theta} \neq \Theta|X = x)f_X(x)dx = \sum\limits_{\theta}P(\hat{\Theta} \neq \Theta|\Theta = \theta)p_{\Theta}(\theta) \]
Continuous $\Theta$, Discrete X

\[ f_{\Theta|X}(\theta|x) = \frac{p_{\Theta}(\theta)p_{X|\Theta}(x|\theta)}{p_X(x)}
\]

\[ p_X(x) = \int\limits_{\theta'}f_{\Theta}(\theta')p_{x|\Theta}(x|\theta')d\theta' \]
- Inferring the unknown bias of a coin and the Beta distribution
Continuous $\Theta$, Continuous X

\[ f_{\Theta|X}(\theta|x) = \frac{f_{\Theta}(\theta)p_{X|\Theta}(x|\theta)}{p_X(x)}
\]

\[ f_X(x) = \int\limits_{\theta'}f_{\Theta}(\theta')p_{x|\Theta}(x|\theta')d\theta' \]
- Linear normal models: estimation of a noisy singal
- Estimating the parameter of a uniform
  
  $X$: uniform $[0, \Theta]$
  
  $\Theta$: uniform $[0, 1]$
- Performance evaluation of an estimator $\hat{\Theta}$
  
  $E[(\hat{\Theta} - \Theta)^2|X = x]$
  
  $E[(\hat{\Theta} - \Theta)^2]$

Useful equation:

\[ \int_0^1 \theta^\alpha(1-\theta)^\beta d\theta = \frac{\alpha!\beta!}{(\alpha + \beta + 1)!}
\]

7.2 Linear models with normal noise

7.2.1 Recognizing normal PDFs

Normal distribution: $X \sim N(\mu, \sigma^2)$

$f_X(x) = \frac{1}{\sigma\sqrt{2\pi}} e^{-(x-\mu)^2/2\sigma^2}$
$f_X(x) = c e^{-(\alpha x^2 + \beta x + \gamma)}$, $\alpha > 0$ Normal with mean $-\beta/2\alpha$ and variance $-1/2\alpha$

7.2.2 Estimating a normal random variable in the presence of additive normal noise

$X = \Theta + W$, $\Theta, W,N :(0,1), independent$

$ \hat{\theta} _{MAP} = \hat{\theta} _{LMS} = E[\Theta|X = x] = x/2$
even with general means and variances:
- posterior is normal
- LMS and MAP estimators conincide
- these estimators are "linear" of the form $\hat{\Theta} = aX + b$

7.2.3 The case of multiple observations

$X_i = \Theta + W_1$, $\Theta \sim N(x_0, \sigma_0^2)$, $W_i \sim N(x_i, \sigma_i^2), \Theta, W_i$ indepedent

$\hat{\theta} _{MAP} = \hat{\theta} _{LMS} = E[\Theta|X = x] = \frac{\sum\limits _{i=0}^n\frac{x_i}{\sigma_i^2}}{\sum\limits _{i=0}^n\frac{1}{\sigma_i^2}}$
Key conclusions
- posterior is normal
- LMS and MAP estimates coincide
- these estimates are "linear" of the form $\hat{\theta} = a_0 + a_1x_1 + \dots + a_nx_n$
Interpretations
- estimate $\hat{\theta}$: weighted average of $x_0$ (prior mean) and $x_i$ (observations)
- weights determined by variances

7.2.4 The mean square error

Performance measures
- $E[(\Theta - \hat{\Theta})^2|X = x] = E[(\Theta - \hat{\theta})^2|X = x] = var(\Theta|X = x) = \frac{1}{\sum\limits _{i=0}^n \frac{1}{\sigma_i^2}}$
- $E[(\Theta - \hat{\Theta})^2] = \int E[(\Theta - \hat{\Theta})^2|X = x] f_X(x) dx = \frac{1}{\sum\limits _{i=0}^n \frac{1}{\sigma_i^2}}$

7.3 Least mean squares (LMS) estimation

7.3.1 In the absence of observations

Least Mean Square formulation: minimize Mean Squared Error (MSE) $E[(\Theta - \hat{\theta})^2]: \hat{\theta} = E[\Theta]$
$E[(\Theta - E[\Theta])^2]:var(\Theta)$

7.3.2 LMS estimation of $\Theta$ based on X

Minimize conditional mean square error: $E[(\Theta - \hat{\theta})^2|X = x]: \hat{\theta} = E[\Theta|X = x]$

7.3.3 LMS performance evaluation

LMS estimate: $\hat{\theta} = E[\Theta|X=x]$
Estimator: $\hat{\Theta} = E[\Theta|X]$
Expected performance, once we have a measurement - Conditional mean square error

$MSE = E[(\Theta - E[\Theta|X=x])^2|X=x] = var(\Theta|X=x)$
Expected perfornamce of the design:

$MSE = E[(\Theta - E[\Theta|X])^2] = E[var(\Theta|X)] = \int var(\Theta|X=x) \cdot f_X(x) dx$ Average of conditional variance
A good example

7.3.4 Properties of the estimation error in LMS estimation

Given Estimator: $\hat{\Theta} = E[\Theta|X]$ and Error: $\tilde{\Theta} = \hat{\Theta} - \Theta$

$E[\tilde{\Theta|X=x}] = 0$
$cov(\tilde{\Theta},\hat{\Theta}) = 0$
$var(\Theta) = var(\hat{\Theta}) + var({\tilde{\Theta}})$

7.4 Linear least mean squares (LLMS) estimation

Motivation: Conditional expectation $E[\Theta|X]$ maybe hard to compute/implement

7.4.1 LLMS formulation

Consider estimators of $\Theta$ of the form $\hat{\Theta} = aX + b$, minimize $E[(\hat{\Theta} - \Theta)^2] \implies E[(\hat{\Theta} - aX - b)^2] $

7.4.2 LLMS solution

Minimize $E[(\hat{\Theta} - \Theta)^2]$, that is $E[(\Theta - aX - b)^2]$

\[ \hat{\Theta}_L = E[\Theta] + \frac{Cov(\Theta,X)}{var(X)}(X - E[X]) = E[\Theta] + \rho \frac{\sigma _\Theta}{\sigma_X}(X - E[X])
\]

$\rho$ corelation coefficiency

Remarks on the solution and on the error variance

Only means, variances, covariances matter (we do not need to know everything)

$E[(\hat{\Theta}_L - \Theta)^2] = (1 - \rho^2)var(\Theta)$

7.4.3 LLMS with multiple observations

Consider the form $\hat{\Theta} = a_1X_1 + \dots + a_nX_n + b$
Minimize $E[(a_1X_1 + \dots + a_nX_n + b - \Theta)^2]$
Solve linear system in $b$ and $a_i$
if $E[\Theta|X]$ is linear in X, then $\hat{\Theta} _{LMS} = \hat{\Theta} _{LLMS}$
suppose general distributions with same mean, variances
- $\hat{\theta} _{MAP} = \hat{\theta} _{LMS} = E[\Theta|X = x] = \frac{\sum\limits _{i=0}^n\frac{x_i}{\sigma_i^2}}{\sum\limits _{i=0}^n\frac{1}{\sigma_i^2}}$
- $\hat{\Theta} _{LMS} = E[\Theta|X] = \frac{\frac{x_0}{\sigma _0^2} + \sum\limits _{i=i}^n\frac{X_i}{\sigma_i^2}}{\sum\limits _{i=0}^n\frac{1}{\sigma_i^2}} = \hat{\Theta} _{LLMS}$

7.5 Bayesian inference summary

Unit 8 Limit theorems and clasic statistics

8.1 Inequalities, comvergence, and the Weak Law of Large Numbers

8.1.1 Markov and Chebyshev inequality

Markov inequality

"If $X \geq 0$ and $E[X]$ is small, then X is unlikely to be very large"

\[ P(X \geq a) \leq \frac{E[X]}{a} \text{, for all } a > 0 \text{ and } X \geq 0 \]
Chebyshev inequality

"If the variance is small, then X is unlikely to be too far from the mean"

\[ P(|X - \mu| \geq c) \leq \frac{\sigma^2}{c^2} \text{, for all } c > 0 \text{ and } X \text{ is a random variable with mean } \mu \text{ and variance } \sigma^2 \]

8.1.2 The Weak Law of Large Numbers (WLLN)

$X_1, X_2, \dots$ i.i.d.: infinite mean $\mu$ and variance $\sigma^2$

\[ \text{Sample mean: } M_n = \frac{X_1 + \dots + X_n}{n} \]

$E[M_n] = \mu$
$Var(M_n) = \frac{\sigma^2}{n}$
WLLN: for $\varepsilon > 0$,

\[ P(|M_n - \mu|) \geq \varepsilon = P \left( \left| \frac{X_1 + \dots + X_n}{n} - \mu\right| \geq \varepsilon \right) \to 0 \text{, as n} \to \infty \]
Interpreting the WLLN
- Sample mean $M_n$ is unlikely to be far off from true mean $\mu$
- Sample mean $M_n$ is the emperical frequency of even $A$, with $p = P(A)$

8.1.3 Convergence in Probability

Sequence of random variables $Y_n$, not necessarily independent

Definition: A sequence $Y_n$ converges in probability to a certain number a if:

\[ \lim_\limits{n \to \infty} P(|Y_n - a| \geq \varepsilon) = 0
\]

Almost all of the PMF/PDF of $Y_n$ eventually gets concentrated (arbitrarily) close to a

Some properties - suppose that $X_n \to a, Y_n \to b$
1. if g is continuous, then $g(X_n) \to g(a)$
2. $X_n + Y_n \to a + b$
3. $E[X_n]$ need not converge to a

8.2 The Central Limit Theorem (CLT)

8.2.2 What exactly does the CLT say?

Theory

$Z_n = \frac{S_n - n\mu}{\sqrt{n}\sigma}$ and $Z \sim N(0,1)$
- CDF of Z_n converges to normal CDF
- results for convergence of PDFs or PMFs (with more assumptions)
- results without assuming that X_i are identically distributed
- results under "weak dependence"
In short, CLT applies to a sequence of random variables that do not need to be i.i.d.
Practice
- The practiec of normal approximations:
  - treat Z_n as if it were normal
  - treat S_n as if normal: $N(n\mu, n\sigma^2)$ as $S_n = \sqrt{n}\sigma Z_n + n\mu$
- Can we use the CLT when n is "moderate"?
  - usually, yes
  - symmetry and unimodality help

8.3 An introduction to classical statistics

8.3.1 Overview

Inference using the Bayes rule:

unknown $\Theta$ and observation $X$ are both random variables: Find $p_{\Theta|X}$
Classical statistics: unknown constant $\theta$
- Problem types in classical statistics
  - Hypothesis testing: $H_0: \theta = 1/2 \text{ vs. } H_1: \theta = 3/4$
  - Composite hypotheses: $H_0: \theta = 1/2 \text{ vs. } H_1: \theta \neq 1/2$
  - Estimation: design an estimator $\hat{\Theta}$, to keep estimation error $(\hat{\Theta} - \theta)$ small.

8.3.2 The sample mean and some terminology

Estimating a mean
- $X_1, \dots, X_n$: i.i.d, mean $\theta$, variance $\sigma^2$
- Sample mean $= \hat{\Theta}_n = M_n = \frac{X_1 + \dots + X_n}{n}$
Properties and terminology
- $E[\hat{\Theta}_n] = \theta$ (unbiased) for all $\theta$
- WLLN: $E[\hat{\Theta}_n] \to \theta$ (consistency) for all $\theta$
- Mean square error (MSE): $E[(\hat{\Theta}_n - \theta)^2] = var(\hat{\Theta}_n) = \frac{\sigma^2}{n}$

8.3.3 On the mean square error of an estimator

\[ E[(\hat{\Theta} - \theta)^2] = var(\hat{\Theta} - \theta) + (E[\hat{\Theta} - \theta])^2 = var(\hat{\Theta}) + (bias)^2
\]

Sample mean estimator ($\hat{\Theta}_n = M_n$): $MSE = \frac{\sigma^2}{n} + 0$
Zero estimator ($\hat{\Theta} = 0$): $MSE = 0 + \theta^2$
$\sqrt{var(\hat{\Theta})}$ is the standard error .

Standard Error refers to sampling distribution, whereas standard deviation refers to sample distribution

8.3.4 Confidence intervals (CIs)

An $1 - \alpha$ confidence interval is an interval $[\hat{\Theta}^-, \hat{\Theta}^+]$, for all $\theta$

\[ P(\hat{\Theta}^- \leq \theta \leq \hat{\Theta}^+)
\]

CI for the estimation of the mean
- $X_1, \dots, X_n$: i.i.d, mean $\theta$, variance $\sigma^2$
- Sample mean $= \hat{\Theta}_n = M_n = \frac{X_1 + \dots + X_n}{n}$
- 95% CI: $\Phi(1.96) = 0.975 = 1 - 0.025$
  
  \[ P \left( \frac{|\hat{\Theta}_n - \theta|}{\sigma/\sqrt{n}}\right) \leq 1.96 \approx 0.95 \text{ (CLT) } \implies P \left(\hat{\Theta}_n - \frac{1.96\sigma}{\sqrt{n}} \leq \theta \leq \hat{\Theta}_n + \frac{1.96\sigma}{\sqrt{n}}\right) \]
CI for the mean when $\sigma$ is unknown
1. use upper bound on $\sigma$
  - for $X_i$ Bernoulli: $\sigma \leq 1/2$
2. use ad hoc estimate of $\sigma$
  - for $X_i$ Bernoulli: $\sigma = \sqrt{\hat{\Theta}_n(1 - \hat{\Theta}_n)}$
3. use sample mean estimate of the variance
  
  $\sigma^2 = E[(X_i - \theta)^2] \implies \frac{1}{n} \sum\limits_{i = 1}^n (X_i - \hat{\Theta}_n)^2 \to \sigma^2$

Two approximations involved here:
- CLT: approximately normal
- using estimate of $\sigma$
correction for second approximation (t-tables) used when n is small.

8.3.5 Other natural estimators

8.3.6 Maximum Likelihood (ML) estimation

Pick $\theta$ that "makes data most likely"

\[ \hat{\theta}_ {ML} = arg \max\limits_{\theta} p_X(x;\theta)
\]

compare to maximum a posterior probability Bayesian posterior $p_{\Theta|X}(\theta^*|x) = \max\limits_{\theta}p_{\Theta|X}(\theta|x)$

Unit 9 The Bernoulli and Poisson process

9.1 The Bernoulli process

9.1.1 Definition

A sequence of independent Bernoulli tirals, $X_i$
At each trial, i:

$P(X_i = 1) = P(\text{success at the ith trial}) = p$

$P(X_i = 0) = P(\text{failure at the ith trial}) = 1 - p$
Properties
- $E[X_i] = p$
- $var(X_i) = p*(1-p)$
Key assumption
- Independence
- Time-homogeneity

9.1.2 Stochastic processes

A sequence of random variables $X_1, X_2, \dots$
Sample space: $\Omega = \text{a set of infinite sequence of 0's and 1's}$

9.1.3. Number of successes/arrivals S in n time slots (Binomial distribution)

$S = X_1 + X_2 + \dots + X_n$
$P(S=k) = \binom{n}{k}p^k(1-p)^{n-k}$, k = 0, 1, 2 ....
$E[S] = np$
$var(S) = np(1-p)$

9.1.4 Time until the first success/arrival (Geometric distribution)

$T_i = min \{i: X_i=1 \}$
$P(T_1 = k) = (1-p)^(k-1)p$, k = 1,2,...
$E[T_1] = \frac{1}{p}$
$var(T_1) = \frac{1-p}{p^2}$

9.1.5 Independence, memorylessness, and fresh-start properties

Fresh-start after time n (slots), after time T1
Fresh-start after a random time N
- N = time of 3rd sucess
- N = first time that 3 successes in a row have been observed
The process $X_{N+1}, X_{N+2}$, ... is
- A Bernoulli process
- independent of N, $X_1, X_2, \dots, X_N$
as long as N is determined "casually"

9.1.6 Time of the kth success/arrival

$Y_k$ = time of kth arrival
$T_k$ = kth inter-arrival time = $Y_k - Y_{k-1} \text{, } k \geq 2 $
$Y_k = T_1 + \dots + T_k$
- The process starts fresh after time T1
- T2 is independent of T1: Geometric(p)
- $E[Y_k] = \frac{k}{p}$
- $var(Y_k) = \frac{k(1-p)}{p^2}$
- PMF: $p_{Y_k}(t) = \binom{t-1}{k-1}p^k(1-p)^{t-k} \text{, } t = k, k +1, ..$.

9.1.7 Merging of independent Bernoulli processes

$X_i$: Bernoulli(p)
$Y_i$: Bernoulli(q)
Merged process: $Z_i: g(X_i, Y_i)$ Bernoulli(p + q - pq)

9.1.7 Splitting of a Bernoulli process

9.1.8 Poisson approximation to binomial

Interesting regime: large n, small p, moderate λ = np
Number of arrivals S in n slots: $p_S(k) \to \frac{\lambda^k}{k!}e^{-\lambda}$ (For fixed k = 0, 1...)

9.2 The Poison process

9.2.1 Definition

Poisson process is similar to Bernoulli process, but in a continuous time interval.

Numbers of arrivals in disjoint time intervals are independent

\\(P(k, \tau)\\) = Prob. of *k* arrivals in interval of duration \\(\tau\\)

Small interval probabilities - For VERY small $\delta$:

\[ P(k, \delta) = \begin{cases} 1-\lambda\delta + O(\delta^2) & \quad \text{if } k = 0 \\ \lambda\delta + O(\delta^2) & \quad \text{if } k=1 \\ 0 + O(\delta^2) & \quad \text{if } k>1 \end{cases} \]

\[ P(k, \delta) \approx \begin{cases} 1-\lambda\delta & \quad \text{if } k = 0 \\ \lambda\delta & \quad \text{if } k=1 \\ 0 & \quad \text{if } k>1 \end{cases} \]

λ: "Arrival rates"

9.2.2 The Poisson PMF for the number of arrivals

$N_{\tau}:\text{ arrivals in }[0, \tau]$
$N_\tau \approx Binomial(n,p)$, $n = \frac{\tau}{\delta}$, $p = \lambda\delta + O(\delta^2)$
\[ P(k, \tau) = P(N_\tau =k) = \frac{(\lambda\tau)^ke^{-\lambda\tau}}{k!}, \text{k = 0, 1, 2,...} \]
$E[N_\tau] \approx np \approx \lambda\tau$
$var(N_\tau) \approx np(1-p) \approx \lambda\tau$

9.2.3 The time $T_1$ until the first arrival

Find the CDF: $P(T_1 \leq t) = 1 - P(T_1 > t) = 1 - P(0,t) = 1 - e^{-\lambda t}$

\[ f_{T_1}(t) = \lambda e^{-\lambda t} \text{, for } t \geq 0
\]

Exponential(λ)

9.2.4 The time $Y_k$ of the kth arrival

Two ways to derive:

Through CDF: $P(Y_k \leq y) = \sum\limits_{n=k}^{\infty}P(n, y)$
More intuitive argument

\[ f_{Y_k}(y)\delta \approx P(y \leq Y_k \leq y + \delta) \approx P(k-1, y)\lambda\delta \]

Erlang distribution

\[ f_{Y_k}(y) = \frac{\lambda^k y^{k-1} e^{-\lambda y} }{(k-1)!} \text{, } y \geq 0
\]

9.2.5 Memorylessness and the fresh-start property

If we start watching at time t, we see Poisson process, independent of the history until time t. Then, time until next arrival follows exp(λ)
Time between first and second arrival, $T_2 = Y_2 - Y_1$ follows exp(λ)
Similar for all $T_k = Y_k - Y_{k-1} \text{, } k \geq 2$
$Y_k = T_1 + \dots + T_k$ is sum of i.i.d. exponentials
- $E[Y_k] = \frac{k}{\lambda}$
- $var(Y_k) = \frac{k}{\lambda^2}$

9.2.6 Bernoulli/Poisson relation

	Poisson	Bernoulli
Times of Arrival	Continuous	Discrete
Arrival Rate	λ per unit time	p per trial
PMF of # of arrivals	\[P(k,\tau) = \frac{(\lambda\tau)^ke^{-\lambda\tau}}{k!} \\E[N_\tau] \approx \lambda\tau \\ var(N_\tau) \approx \lambda\tau\]	\[P_S(k) = \binom{n}{k}p^k(1-p)^{(n-k)} \\ \to \frac{\lambda^k}{k!}e^{-\lambda} \\ E[S] = np \\ var(S) = np(1-p) \]
Interarrival Time Distr.	\[f_{T1}(t) = \lambda e^{-\lambda t}\] Exponential \[E[T_1] = 1/\lambda \\ var(T_1) = 1/\lambda^2\]	\[P_{T1} = (1-p)^{n-1}p\] Geometric \[E[T_1] = 1/p \\ var(T_1) = \frac{1-p}{p^2}\]
Time to k-th arrival	\[f_{Y_k}(y) = \frac{\lambda^k y^{k-1} e^{-\lambda y}}{(k-1)!}\] Erlang \[E[Y_k] = k/\lambda \\ var(Y_k) = k/\lambda^2\]	\[p_{Y_k}(t) = \binom{t-1}{k-1}p^k(1-p)^{t-k}\] Pascal

9.3 More on the Poisson process

9.3.1 The sum of independent Poisson random variables

\[ P(k, \tau) = \frac{(\lambda\tau)^k e^{-\lambda\tau}}{k!} \]

We call it a Poisson random variable with parameters $\lambda\tau$

The sum of independent Poisson random variables, with means/parameters $\mu$ and $\nu$ is Poisson with mean/parameter $\mu + \nu$

9.3.2 Merging independent Poisson processes

	0 $1 - \lambda_1\delta$	1 $\lambda_1\delta$	≥ 2 $O(\delta^2)$
0 $1 - \lambda_2\delta$	$(1-\lambda_1\delta)(1-\lambda_2\delta)$	$\lambda_1\delta(1-\lambda_2\delta)$	-
1 $\lambda_2\delta$	$\lambda_2\delta(1-\lambda_1\delta)$	$\lambda_1\lambda_2\delta^2$	-
≥ 2 $O(\delta^2)$	-	-	-

0 Arrivals $\approx 1 - (\lambda_1 + \lambda_2)\delta$
1 Arrivals $\approx (\lambda_1 + \lambda_2)\delta$
≥ 2 Arrivals $O(\delta^2)$

Merging independent Poisson(λ1) and Poisson(λ1) result in Poisson(λ1 + λ2))

9.3.3 The time the first(last) light bulb burns out - min{X,Y,Z} and max{X,Y,Z} problem

Three lightbulbs have independent lifetimes X, Y, Z exponential(λ)

The expected time until first lightbulb burnout:
- X, Y, Z: first arrivals in independent Poisson processes
- Merged process: Poisson(3λ)
- min{X, Y, Z}: 1st arrival in merged process $\to E[min] = 1/3\lambda$
The expected time until the last lightbulb burnout:
- Merged process in different intervals
\[ E[max] = \frac{1}{3\lambda} + \frac{1}{2\lambda} + \frac{1}{\lambda} \]

9.3.4 Splitting of a Poisson process

Split arrivals into two streams using independent coin flips of a coin with bias q

Assume that coin flips are independent from the original Poisson process

Resulting streams are Poisson with rate $\lambda q, \lambda (1-q)$
The splitted Poisson processes are independent!

9.3.5 'Random incidence' in the Poisson process

Analysis
Random incidence "Paradox" is not special to the Poisson process
- Example: interarrival times, i.i.d., equally likely to be 5 or 10 mins. Then expected value of k-th interarrival time = 7.5
- Show up at a "random time"
  - P(arrival duaring a 5-minute interarrival interval) = 1/3
  - Expected length of interarrival interval during which you arrive ≈ 8.3
- Sampling method matters - Different sampling methods can give different results
  - Average family size? (3 families with one person, 1 family with 6 persons)
    - look at a random family: 3/4x1 + 1/4x6
    - looat at a random persons's family: 3/9x1 + 6/9x6
  - Average bus occupancy?
  - Average class size?

9.4 Additional theoretical background

9.4.1 Poisson versus normal approximation to the binomial

We have seen that a binomial random variable with parameters n and p can be approximated by a normal random variable (central limit theorem) but also by a Poisson random variable. Are these two facts contradictory? Fortunately not; the two approximations apply to different regimes:

if we fix p and let $n \to \infty)$, we are in the setting where the central limit theorem applies.
If we let $n \to \infty)$, $p \to 0)$, while keeping the product np fixed, the Poisson approximation applies.
If p is very small but np is very large, then two approximations agree.

9.4.2 Sums of a binomial and a Poisson-distributed number of Bernoulli r.v.'s

Let $X_1,X_2,...$ be independent Bernoulli random variables with parameter p, and N be a random variable that takes integer values and is independent of $X_i, i = 1,2, \dots$ Let $Y=X_1+X_2+ \dots +X_N$ for positive values of N, and let $Y =0$ when $N=0$.

If N is binomial with parameters m and q, then Y is binomial with parameters m and pq.
If N is poisson with parameters $\lambda$, then Y is Poisson with parameter $\lambda$.

9.4.3 Sums of a geometrically-distributed number of geometric and exponential r.v.'s

Let N be a geometric random variable with parameter q, and let $X_1, X_2, \dots$ be random variables that are independent and independent of N. Let $Y=X_1+\dots+X_N$.

If $X_i$ is geometric with parameter p, then Y is geometric with parameter pq
If $X_i$ is exponential with parameter $\lambda$, then Y is exponential with parameter $\lambda q$

Inferential Statistics

Here is the course link!

Summary of leaning objectives for each section

1 CLT and Sampling

1.1 Sampling Variability and CLT

1.1.1 Sample distribution and sampling distribution

Sample distribution: sample mean and sample variability (standard deviation)
Sampling distribution

population mean ($\mu $) and population standard deviation ($\sigma$)

\[ \mu = \frac{x_1 + x_2 + ... + x_N}{N} \]

\[ \sigma = \sqrt{\frac{\sum\limits_{i=1}^{N}(x_i - \bar{x})^2}{N}} \]

Most of time, population standard deviation $\sigma$ is not known. Thus, $\sigma$ is usually replaced by sampling standard deviation s
- mean($\bar{x}) \approx \mu $
- standard error: $SE = \frac{\sigma}{\sqrt{n}}$ < $\sigma$

The link to check up the shape of population distribution

1.1.2 Central Limit Theorem (CLT)

The distribution of sample statistics is nearly normal, centered at the population mean, and with a standard error equal to the population standard deviation divided by square root of the sample size.

\[ \bar{x} \sim N(mean = \mu, SE = \frac{\sigma}{\sqrt{n}}) \]

$N$ refers to the shape of distribution, meaning normal distribution.

$\sigma$ is usually unknown, so s is used to replace $s$ - sampling standard deviation

1.1.3 Other important concepts and rules

standard deviation ($\sigma$) vs. standard error (SE)
- $\sigma$ measures the variability in the data
- SE measures the variability in the sample mean (point estimates)
sample size increases -> SE decreases (either from conceptual or mathematically $SE = \frac{\sigma}{\sqrt{n}}$ point of view)
To reduce skewness, either increase sample size (observations) or number of samples
Sampling distribution will be nearly normal only if (the condition of CLT)
- the sample size is sufficiently large (n ≥ 30 or even larger if the data are considerably skewed) or the population is known to have a normal distribution
- the observations in the sample are independent: random sample/assignment and n < 10% of population if sampling without replacement

1.2 Confidential Intervals

1.2.1 Confidential Intervals

confidence interval is defined as the plausible range of values for a population parameter.

confidence level is defined as the percentage of random samples which yield confidence intervals that capture the true population parameter.

confidence interval for a population mean:

\[ \bar{x} \pm z\frac{s}{\sqrt{n}}
\]

margin of error (ME) = $z\frac{s}{\sqrt{n}} $

for 95% CI: $\bar{x} \pm 2SE$ i.e., $ME = 2SE$

conditions for this confidence interval is the same as conditions for CLT (independent and sample size)

z-table

1.2.2 z-score (not covered in the course)

z-score for a single value

Given we know the population parameters ($\mu$ and $\sigma$), calculate z-score for any individual in the population:

\[ z = \frac{(x - \mu)}{\sigma}
\]

Using z-table, the probability can be calculated.
z-score for a sample mean

\[ z = \frac{(\bar{x} - \mu)}{\frac{\sigma}{\sqrt{n}}}
\]
Empirical rule
- 68% of values fall within 1 SE of the mean
- 95% fall within 2 SE of the mean
- 99% fall within 3 SE of the mean

1.2.3 Accuracy vs. Precision

Accuracy: whether or not the CI contains the true population paramter.
Precision: the width of a confidence intervals.

Increasing CL, accuracy increases but precision decreases.

To get a higher precision and high accuracy - increase sample size

1.2.3 Required sample size for ME

\[ ME = z \frac{s}{\sqrt{n}} \rightarrow n = \Bigg(\frac{z s}{ME}\Bigg)^2 \]

1.3 R vs. sampling distribution

Load the package and dataset(ames)

    library(statsr)
    library(dplyr)
    library(shiny)
    library(ggplot2)

    data(ames)

Distribution of areas of homes and summary statistics

ames %>%
    summarise(mu = mean(area), pop_med = median(area), 
        sigma = sd(area), pop_iqr = IQR(area),
        pop_min = min(area), pop_max = max(area),
        pop_q1 = quantile(area, 0.25),  # first quartile, 25th percentile
        pop_q3 = quantile(area, 0.75))  # third quartile, 75th percenti

Sample randome 50 houses and calculate the average area

samp1 <- ames %>%
    sample_n(size=50)

samp1 %>%
    summarise(x_bar = mean(area))

# or combine above two code chunks into one
samp1 <- ames %>%
    sample_n(size=50) %>%
        summarise(x_bar = mean(area))

Estimate population mean by using sampling distribution

Take 15,000 samples of size 50 from the population (rep_sample_n), calculate the mean of each sample, and store each result in a vector called 'sample_means50'.

sample_means50 <- ames %>%
  rep_sample_n(size = 50, reps = 15000, replace = TRUE) %>%
    summarise(x_bar = mean(area))

ggplot(data = sample_means50, aes(x = x_bar)) +
  geom_histogram(binwidth = 20)

To get the summary statistics of 15,000 sample means, analyze the statistics from the 'sample_means50', which is actually a dataset containing 15,000 observations(x_bar).

sample_means50 %>%
    summarise(sampling_x_bar = mean(x_bar))

1.4 Python vs. sampling distribution

Load packages and import dataset

import pandas as pd
import numpy as np
import random as random
import math
import matplotlib.pyplot as plt

ames = pd.read_csv("/content/drive/MyDrive/Colab Notebooks/ames.csv")
#ames.head
#ames.columns

Distribution of population

mu = np.average(ames["Lot.Area"])
sigma = np.std(ames["Lot.Area"])

plt.hist(ames["Lot.Area"],30, range=[0, mu+5*sigma])
plt.show()
#right skewed distribution

Randomly take 10 samples

samp1 = ames.sample(n=10,replace=True)

Take 1000 samples with size 200

size = 200
num_samp = 1000
samp_mean = []

for m in range(num_samp):
  samp = ames.sample(n=size,replace=True)
  x_bar_samp = np.average(samp["Lot.Area"])
  samp_mean.append(x_bar_samp)
  m += 1

x_bar_samp_mean = np.average(samp_mean)
x_bar_samp_se = np.std(samp_mean)/(math.sqrt(size))

print(x_bar_samp_mean)
print(x_bar_samp_se)

plt.hist(samp_mean, 20, range=[5000,15000])
plt.show()

2 Hypothesis testing and significance

2.1 Hypothesis testing (for a mean)

Null hypothesis - $H_0$
Alternative hypothesis - $H_A$

The hypothesis is always about pop.parameters, never about sample statistics (because the sample statistics is certain).

p-value - P(observed or more extreme outcome | $H_0$ true)

Given $n = 50, \bar{x} = 3.2, s = 1.74, SE = 0.246$

We are looking for $P(\bar{x} > 3.2 | H_0 : \mu = 3) $

Since we believe that null hypothesis is true, $\bar{x} \sim N(\mu = 3, SE = 0.246)$ based on the CLT.

test statistics: z-score = (3.2-3)/0.246 = 0.81, which is used to calculate the p-value (the probability of observing data at least favorable to the alternative hypothesis as our current data set, if the null hypothesis was true)

p-value = P(z > 0.81) = 0.209

Decision based on the p-value

p-value < the significant level, $\alpha$ (usually 5%): it is unlikely to observe the data if the null hypothesis is true: Reject $H_0$
p-value ≥ $\alpha$: it is likely to occur even if the null hypothesis were true: Do no reject $H_0$

two-sided(tailed) tests

In the same case, $P(\bar{x} > 3.2 \text{ or } \bar{x} > 2.8| H_0 : \mu = 3) $

p-value = $P(z > 0.81) + P(z < -0.81) = 0.418 $ --- fail to reject $H_0$.

2.2 Significance

2.2.1 Inference for other estimators

point estimates:

$\hat{\theta}$: $\hat{\theta}_{LMS}$ or ($\hat{\theta} _{MAP}$) the concept might be different from MIT statistics course
1. sample mean
2. difference between sample means
3. sample proportion $\hat{p}$
4. difference between two proportions
two requirements:
- nearly normal sampling distribution
- unbiased estimator assumption: point estimates are unbiased, i.e., the sampling distribution of the estimate is centered at the true population parameter it estimates.

2.2 Decision errors

Decrease significance level ($\alpha$) decrease Type I error rate

$P(\text{Type I error}|H_0 \text{ true}) = \alpha$

Choosing $\alpha$
- if Type I error is dangerous or costly, choose a small significance level (e.g. 0.01)
- if Type II error is dangerous or costly, choose a high significance level (e.g. 0.10)

$\beta$ depends on the effect size $\delta$ - difference between point estimate and null value.

2.2.3 Significance level vs. confidence level

complement each other depending on one-sided or two -sided tests
- two-sided tests: Significance level = 1 - confidence level
- one-sided tests: Significance level ≠ confidence level
  
  CL = 1 - 2 x alpha

2.2.4 Statistical vs. practical significance

practical significance

Real difference between point estimator and null value are easier to detect with larger samples (effect size)
statistical significance

very large samples will result in statistical significance even for tiny differences between sample mean and the null value (effect size), even when the difference is not practically significant.

3 Inference for Comparing Means

3.1 t-distribution and comparing two means

3.1.1 t-distribution

What purpose does a large sample serve?

As long as observations are independent, and the population distribution is not extremely skewed, a large sample would ensure that

the sampling distribution of the mean is nearly normal.
the estimate of the standard error is reliable: $\frac{s}{\sqrt{n}}$

t-distribution

when σ unknown(almost always), use the t-distribution to address the uncertainty of the standard error estimate
bell shaped but thicker tails than the normal
- observations more likely to fall beyond 2 SDs from the mean
- extra thick tails helpful for mitigating the effect of a less reliable estimate for the standard error of the sampling distribution
always centered as 0
only has one parameter degress of freedom(df) to determine the thickness of tails: higher df, less thick the tail

the normal distribution has two parameters: mean and SD
for inference on a mean where σ unknown, the calculation is the same way as normal distribution

\[ T = \frac{\text{obs - null}}{SE} \]
- find p-value (one or two tail area, based on $H_A$)

3.1.2 Inference for a mean

estimating the mean = point estimate ± margin of error

\[ \bar{x} \pm t_{df}^*SE_{\bar{x}} \\ SE_{\bar{x}} = \frac{s}{\sqrt{n}} \]

degrees of freedome for t statistic for inference on one sample mean

\[ df = n - 1
\]

3.1.3 Inference for comparing two independent means

estimating the mean = point estimate ± margin of error

\[ (\bar{x_1} - \bar{x_2}) \pm t_{df}^*SE_{(\bar{x_1} - \bar{x_2})} \]

SE of difference between two independent means

\[ SE_{(\bar{x_1} - \bar{x_2} )}= \sqrt{\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}} \]
DF for t statistics for inference on difference of two means

\[ df = min(n_1-1, n_2-1) \]

Conditions for inference for comparing two independent means
1. independence:
```
 - within groups: 

 - random sample/assignment

 - if samping without replacement, n < 10% of population

 - between groups: not paired
```
1. Sample size/skew: the more skew in the population distributions, the higher the sample size needed.

3.1.4 Inference for comparing two paried means

When two sets of observations have a special correspondence(not independent), they are said to be paired.

Two analyze paired data, it is often useful to look at the difference in outcomes of each pair of observations.

Parameter of interest: $\mu_{diff}$ - average difference between the reading and writing scores of all high school students
Point estimate: $\bar{x}_{diff}$ - average difference between the reading and writing scores of sampled high school students
$SE = \frac{s_{diff}}{n}$

Summary

paired data (2 var.) $\to$ differences (1 var.)
most often: $H_0:\mu_{diff} = 0$
same individuals: pre-post studies, repeated measures, etc.
different but dependent individuals: tiwns, partners, etc.

3.1.5 Power

Power of a test is the probability of correctly rejecting H0, and the probability is $1-\beta$

Practical problem 1: calculate power for a range of sample sizes and choose target power

Practical problem 2: calculate required sample size for a desired level of power

3.2 ANOVA and Bootstrapping

3.2.1 Comparing more than two means -- F distribution

ANOVA (analysis of variance) test

$H_0$: the mean outcome is the same across all categories
$H_A$: at least one pair of means are different from each other

t-test	ANOVA
compute a test statistic (a ratio)	Compute a test statistic (a ratio)
\[t = \frac{(\bar{x_1}-\bar{x_2})-(\mu_1-\mu_2)}{SE_{(\bar{x_1}-\bar{x_2})}}\]	\[F = \frac{\text{variability bet. groups}}{\text{variability within groups}}\]

In order to be able to reject $H_0$, we need a small p-value, which requires a large F statistic.
Obtaining a large F statistic requires that the variability between sample means is greater than the variability within the samples.

3.2.2 ANOVA

variability partitioning
ANOVA Output

ANOVA Output table
- The first row is about between group variability (Group row) and the second the row is the within group variability (Error row)
- Sum square error
```
 - Total: sum of squares total (SST) measures the total variability in the response variable. The caculation is very similar to that of variance except for no dividing by the sample size.

 \\[
 SST = \sum\limits_{i=1}^n (y_i-\bar{y})^2 
 \\]

 \$y_i\$: value of the response variable for each observation

 \$\bar{y}\$: grand mean of the response variable

 - Group: sum of squares groups (SSG) measures the variability between groups. Explained variability: squared deviation of group means from overall mean, weighted by sample size. 

 \\[
 SSG = \sum\limits_{j=1}^k n_j(\bar{y_j}-\bar{y})^2 
 \\]

 \$n_j\$: number of observations in group *j*

 \$y_j\$: mean of the response variable for group *j*

 \$\bar{y}\$: grand mean of the response variable

 - Error: sum of squares error (SSE) measures the variability within groups. Unexplained variability: unexplained by the group variable due to other reasons

 \\[
 SSE = SST - SSG 
 \\]
```
- DF: degree of freedom
- Mean square error: average variability between and within groups, calculated as the total variability (sum of squares) scaled by the associated degrees of freedom.
 - group: MSG = SSG/DF_G
 - error: MSE = SSE/DF_E
- F statistics: ratio of the average between group and within group variabilities
 
 \[ F = \frac{MSG}{MSE}
 \]
- Calculate p-value according to F statistics, and remember F always positive we only calculate one-tail.
 - if p-value is small (less than $\alpha$): reject H0
 
 The data provide convincing evidence that at least one pair of population means are different from each other (but we cannot tell which one)
 - if p-value is large (larger than $\alpha$): fail to reject H0
 
 The data do not provide convincing evidence that at least one pair of population means are different from each other; the observed difference in sample means are attributable to sampling variability (or chance)

3.2.3 ANOVA conditions

Independence: between groups and within groups
Approximate normality: distributions should be nearly normal within each group
constant variance: groups should have roughly equal variability

side-by-side boxplot is helpful to check constant variance condition

3.2.4 Multiple comparisons

Bonferroni correction: adjust $\alpha$ by the number of comparison being considered K

\[ K = \frac{k(k-1)}{2} \\ \alpha^* = \alpha/K
\]
Pairwise comparisons:
- constant variance $to$ use consistent standard error and degrees of freedom for all tests
- compare p-values from each test to the modified significance level
- Standard error for multiple pairwise comparisons:
  
  \[ SE = \sqrt{\frac{MSE}{n_1}+\frac{MSE}{n_2}} \]
  
  compared to t test between two independent groups $SE = \sqrt{\frac{S_1^2}{n_1}+\frac{S_2^2}{n_2}}$
- Degrees of freedom for multiple pairwise comparisons: df = df_E
  
  compared to t test: df = min(n₁ - 1, n₂ - 1)

3.2.5 Bootstrapping

Bootstrapping scheme:
1. take a bootstrap sample - a random sample taken with replacement from the original sample, of the same size as the original sample
2. calculate bootstrap statistic - mean, median, proportion, etc. computed on the bootstrap samples.
3. repeat steps 1 and 2 many times to create a bootstrap distribution - a distribution of bootstrap statistics.
calculate confidence interval:
1. percentile method
2. standard error method
limitations
- not as rigid conditions as CLT based methods
- if bootstrap distribution is extremely skewed or sparse, the bootstrap interval might be unreliable
- A representative sample is still needed - if the sample is biased, the estimates resulting from this sample will also be bias.

Bootstrap vs. sampling distribution

sampling distribution: created using sampling with replacement from the population
Bootstrap distribution: created using sampling with replacement from the sample
Both are distributions of sample statistics

4 Inference for Proportion

Categorical variables oppose to numerical variables

one categorical variable:
- two levels: success-failure
- more than two levels
two categorical variables:
- two levels: success-failure
- more than two levels

4.1 Inference for proportions

4.1.1 Sampling Variability and CLT for Proportions

For numerical variables, sample statistic from sampling distribution is mean

For categorial variables, sample statistic from sampling distribution is proportion

CLT for proportions: The distribution of sample proportion is nearly normal, centered at the population proportion, and with a standard error inversely proportional to the sample size.

\[ \hat{p} \sim N \left( mean=p, SE=\sqrt{\frac{p(1-p)}{n}}\right) \]

Conditions for the CLT
- Independence
- Sample size/skew: there should be at least 10 successes and 10 failures in the sample: np ≥ 10 and n(1-p) ≥ 10.
What if the success-failure condition is not met:
- the center of the sampling distribution will still be around the true population proportion
- the spread of the sampling distribution can still be approximated using the same formula for the standard error
- the shape of the distribution will depend on whether true population proportion is close to 0 (righ skew) or to 1 (left skew).

4.1.2 Confidence interval for a proportion

parameter of interest: $p$
point estimate: $\hat{p}$ sample proportion
estimating a proportion: point estimate ± margin of error

\[ \hat{p} = z^* SE_{\hat{p}}
\]
- SE for a proportion for calculating a confidence interval:
  
  \[ SE_{\hat{p}} = \sqrt{\frac{\hat{p}(1-\hat{p})}{n}} \]
- calculating the required sample size for desired ME
  - use $\hat{p}$ from previous study
  - if no previous study, use $\hat{p} = 0.05$ as it gives the most conservative estimate - highest possible sample size

4.1.3 Hypothesis testing for a proportion

set the hypothesis
calculate the point estimate $\hat{p}$
Check conditions
Draw sampling distribution, shade p-value, calculate test statistic.
Make a decision based on the research context.

Null hypothesis always contains a "=" sign.

4.1.4 Estimating the Difference Between Two Proportions

calculating a confidence interval for the difference between the two population proportions that are unknown using data from our sample

Estimating the difference between two proportions:

\[ (\hat{p}_1 - \hat{p} _2) \pm z^* SE _{(\hat{p}_1 - \hat{p}_2)} \\ SE = \sqrt{\frac{\hat{p}_1(1-\hat{p}_1)}{n_1} + \frac{\hat{p}_2(1-\hat{p}_2)}{n_2}}
\]
conditions for inference for comparing two independent proportions
1. Independent: within groups and between groups
2. Sample size/kew: each sample should meet the success-failure condition

4.1.5 Hypothesis Test for Comparing Two Proportions

pooled proportion $H_0: p_1 = p_2 = $ pooled proportion

\[ \hat{p}_{pool} = \frac{\text{total successes}}{\text{total n}}
\]

4.2 Simulation based inference for proportions and chi-square testommg

4.2.1 Small sample proportion

which does not meet success-failure condition

inference via simulation
setting up a simulation assuming H0 true
- the ultimate goal of a hypothesis test is a p-value
- devise a simulation scheme that assumes the null hypothesis is true
- repeat the simulation many times and record relevant sample statistic CLT?
- calculate p-value as the proportion of simulations that yield a result favorable to the alternative hypothesis

4.2.2 Comparing Two Small sample proportions

For comparing two proportions with hypothesis test, the pooled proportion should be used.

4.2.3 Chi-Square GOF test

Deals with data with one category with more than two levels to a hypothesis distribution

goodness of fit

test is to evaluate how well the observed data fit the expected distribution

Conditions for the Chi-Sqaure test:
- Independence
 - random sample/assignment
 - if sampling without replacement, n < 10% of population
 - each case only contributes to one cell in the table
- Sample size: each particular scenarior (i.e., cell) must have at least 5 expected cases.
Anatomy of a test statistic

General form of a test statistic

\[ \frac{\text{point estimate - null value}}{\text{SE of point estimate}}
\]
1. identifying the difference between a point estimate and an expected value if the null hypothesis were true
2. standardizing that difference using the standard error of the point estimate
Chi-Square $\chi$ statistic: dealing with counts and investigating how far the observed counts are from the expected counts

\[ \chi^2 = \sum\limits_{i=1}^{k}\frac{(O-E)^2}{E}
\]

O: observed

E: expected

k: number of cells
Chi-Square $\chi$ distribution: has just one parameter
- degrees of freedom (df): influence the shape, center and spread
p-value
- p-value for a chi-square test is defined as the tail area above the calculated test statistic
- the test statistic is always positive, and a higher test statistic means a higher deviation from the null hypothesis

4.2.4 Chi-Square independence test

Deals with two categorial variables at least one with > 2 levels

Chi-square independence test is to evaluate the relationship between two categorical variables

\[ \chi^2 = \sum\limits_{i=1}^{k}\frac{(O-E)^2}{E}
\]

df = (#rows - 1)x(#columns - 1)
the same conditions as chi-square GOF test

4.3 Assumption consistency

One Population Proportion

Sample can be considered a simple random sample
- Large enough sample size ()
  - Confidence Interval: At least 10 of each outcome ()
  - Hypothesis Test: At least 10 of each outcome ()
Two Population Proportions
- Samples can be considered two simple random samples
- Samples can be considered independent of one another
  - Large enough sample sizes ()
  - Confidence Interval: At least 10 of each outcome ()
  - Hypothesis Test: At least 10 of each outcome () - Where (the common population proportion estimate)
One Population Mean
- Sample can be considered a simple random sample
- Sample comes from a normally distributed population
  - This assumption is less critical with a large enough sample size (application of the C.L.T.)
One Population Mean Difference
- Sample of differences can be considered a simple random sample
- Sample of differences comes from a normally distributed population of differences
  - This assumption is less critical with a large enough sample size (application of the C.L.T.)
Two Population Means
- Samples can be considered a simple random samples
- Samples can be considered independent of one another
- Samples each come from normally distributed populations
  - This assumption is less critical with a large enough sample size (application of the C.L.T.)
    - Populations have equal variances – pooled procedure used
    - If this assumption cannot be made, unpooled procedure used

Statistics with Python

1 Introduction to Probability and Statistics

1.1 Probability Theory

Use Python to simulate coin tossing problem,

# Generate the sum of k coin flips, repeat that n times
def generate_counts(k=1000, n=100):
  X=2*(np.random.rand(k,n)>0.5)-1 # generate a kXn matrix of +-rando
  S=np.sum(X, axis=0)
  return S
coins_flip = generate_counts()

# plot a histogram
plt.style.use('ggplot')
plt.hist(coins_flip, 10, range = [-400, 400])
plt.show

np.random.rand(k,n)>0.5 generate a True/False (k,n) matrix, but it transforms to an integer matrix with 2*

In most cases, we can approximate probabilities using simulations (Monte-Carlo simulations)
However, calculating the probabilities is better because it provides a precise answer and is much faster than Monte-Carlo simulations.

1.2 What is statistics?

Statistics is about analyzing real-world data and drawing conclusions.

The logical of Statistic inference

To answer the question "whether the coin is biased given 570 heads after tossing 1000 times",

Suppose that the coin is fair
Use probability theory to compute the probability of getting at least 570 (or 507) heads
If this probability is very small, then we can reject with confidence the hypothesis that the coin is fair.

Given $x_i = -1$ for tails and $x_i = +1$, we looked at the sum $S_k = \sum_{i=1}^{k} x_i$

If number of heads = 570, then $S_{1000} = 140$

It is known that it is unlikely that $|S_k| > 4 \sqrt{k}$, that is $|S_{1000}| > 4 sqrt{1000} \approx 126.5$
```
from math import sqrt
4*sqrt(1000)
```
Therefore, it is very unlikely that the coin is unbiased. -> the coin is probably biased.

1.3 Three card puzzle

Three cards in a hat

Suppose we have three cards in a hat:

'R''B' - one card is painted blue on one side and red on the other
'R''R' - one card is painted blue on both sides
'B''B' - one card is painted red on both sides

I pick one of the three cards at random, flip it to a random side, and place it on the table. If the other side of the card has a different color I pay you $1; if not you pay me $1.

Monte Carlo simulation


red_bck="\x1b[41m%s\x1b[0m" 
blue_bck="\x1b[44m%s\x1b[0m"
red=red_bck%'R'
blue=blue_bck%'B'
Cards=[(red,blue),(red,red),(blue,blue)]
counts={'same':0,'different':0}

for j in range(50):
    i=int(np.random.rand()*3.) # Generate a random integer in an array [0,1,2] indicating three cards
    side=int(np.random.rand()*2.) # Generate either 0 or 1 indicating the color
    C=Cards[i]
    if(side==1): # select which side to be "up" ('red' is "up")
        C=(C[0],C[1]) # two sides of the selected cards
    same = 'same' if C[0]==C[1] else 'different' # count the number of times the two sides are the same or different.
    counts[same]+=1
    print(''.join(C)+' %-9s'%same, end='')
    if (j+1)%5==0:
    print()
print()
print(counts)

2 Elements, sets and membership

2.1 Basic concepts

Common sets

Intergers {..., -2, -1, 0, 1, 2, ...} $Z$
Naturals {..., 0, 1, 2, 3, ...} $N$
Positives {1, 2, 3, ...} $P$
Rationals {interger ratios m/n, $n \neq 0$} $Q$
Reals {...Google...} $R$

The order and repetition do no matter:
- {0,1} = {1,0}
- {0,1,1,1} = {0,1}

Special sets

Empty set: $x \notin \varnothing$
Universal set: $\forall x \in \Omega$

Define a set in python
- Define a set: set1={1,2} or set2=set({2,3})
- Define an empty set: set() or set({})
Membership - in and not in
Test empty - not

S = set()
not S
#Output: True

Set size - len()

2.2 Basic sets

2.2.1 Sets within Sets

{$x \in A | .... $} = {elements in A such that}

Integer Intervals

$N = \{ x \in Z | x \geq 0 \}$, $P = \{ x \in Z | x > 0 \} $
Real intervals

$[a,b] = \{ x \in R | a \leq x \leq b \}$

$(a,b) = \{ x \in R | a < x < b \}$
Divisibility

Sets of Multiples

$m \in Z$, $_m Z = \{ i \in Z : m| i \}$

Even numbers: $_2 Z = \{ ..., -4, -2, 0, 2, 4, ... \} = E$

Python syntax

{0,...,n-1}: range(n)
{m,...,n-1}: range(m,n)
{m, m+d, m+2d, ...} < n-1: range(m, n, d)

print(set(range(3)))
#Output: {0, 1, 2}

print(set(range(2,5)))
#Output: {2, 3, 4}

print(set(range(2,12,3)))
#Output: {2, 5, 8, 11}
#Return type range, but conver to set if print

2.2.2 Visualization - Venn Diagram

import matplotlib.pyplot as plt
import matplotlib_venn as venn
S = {1, 2, 3}
T = {0, 2, -1, 5}
venn.venn2([S, T], set_labels=('S','T'))
plt.show()

#for 3 sets: venn.venn3([S,T,U], set_labels=(’S’,’T’,'U'))

2.3 Relations

2.3.1 Number relations

Equality - = or ≠
Intersection - two sets share at least one common element

Disjoint - no shared elements
Subsets - $A \subseteq B$

superset - $B \supseteq A$

\[ P \subseteq N \subseteq Z \subseteq Q \subseteq R \]

strict subset - if $A \subseteq B$ and $A \neq B$, A is a strict subset of B, denote $A \subset B$; conversely, A is a strict superset of B, $B \supset A$

2.3.2 Belongs to ($ \in $) vs. Subsets of ($\subseteq $)

$ x \in A $: element x belongsto set A

$ 0 \in \{0,1\} $
($ A \subseteq B $): A is a subset of B

$ \{ 0 \} \subseteq \{0,1\} $

2.3.3 Python syntaxt

Check equality and disjoint

==, !=, .isjointed()

S1={0,1}; S2=set({0,1}); S3={1,0,1}; T={0,2}

# Equality
S1 == T
#Output: False
S1 == S2
S1 == S3
#Output: True

# Inequality
S1 != S2

# Disjoint 
S1.isdisjoint(T)
S1.isdisjoint({2})

Check subsets and supersets

<= or issubset for $\subseteq $ and < for $\subset $

>= or issuperset for $\supseteq $

zero = {0}; zplus = {0,1}; zminus = {0, -1}

print(zminus <= zplus)
#Output: False
print(zminus >= zplus)
#Output: False

zero.issubset(zminus)
#Output: True

2.4 Operations

2.4.1 Intersection and complement

Commutative: $A \cap B = B \cap A$, $A \cup B = B \cap A$
Associative: $(A \cap B) \cap C = A \cap (B \cap C)$, $(A \cup B) \cup C = A \cup (B \cup C)$
Distributive: $A \cap (B \cup C) = (A \cap B) \cup (A \cap C)$, $A \cup (B \cap C) = (A \cup B) \cap (A \cup C)$
De Morgan $(A \cap B)^c = A^c \cup B^c$, $(A \cup B)^c = A^c \cap B^c$

2.4.2 Set Difference A-B

$A-B = \{ x: x \in A \wedge x \notin B \} = A \cap B^c$

Symmetric Difference

The symmetric differene of two sets is the set of elements in exactly one set.

$A bigtriangleup B = \{x: x \in A \wedge x \notin B \vee x \in B \wedge x \notin A \} $

2.4.3 Python Syntax

Union and Intersection

Union $\cup$: | or union

A = {1,2}
B = {2,3}

print(A|B)

C = A.union(B)
print(C)

Intersection $\cap$: & or intersection

print(A&B)

C = A.intersection(B)
print(C)

Set- and Symmetric-Difference

Set difference: - or difference

A = {1,2}
B = {2,3}

A - B

C = B.difference(A)
print(C)

Symmetric difference: ^ or symmetric_difference

A^B

C = B.symmetric_difference(A)
print(C)

2.4.4 Caetesian products

Set: Order and repetition do not matter {a,b,c} = {b,a,c}
Tuple: Both order and reperition matter (a,b,c) ≠ (b,a,c) and (a,a,a) ≠ (a)
- n-tuple: Tuple with n elements
- 2-tuple: Ordered pair (a,b)

Cartesian products

The cartesian product of A and B is the set AxB of ordered pairs (a,b) where a $\in A$ and b $\in B$

\[ A \times B = \{(a,b): a \in A, b \in B \}
\]

$A \times A$ denotes $A^2$
$R^2 = \{(x,y): x,y \in R\} $ - Cartesian Plane
$A, B \subseteq R $ then $A \times B \subseteq R^2 $ - Rectangle
$A \times B = \{(x,y): x \in [0,2], y \in [1,4] \}$, where A = [0,2] and B = [1,4]

Discrete sets

Tables

Tables are Cartesian products

Cartesian product of 3 sets

A x B - 2D

A x B x C - 3D

Sequence

Sequence is tuples just without '()' and some times without ','

Cartesian products with Python

from itertools import product

Faces = set({'J', 'Q', 'K'})
Suits = {'♢','♡'}
for i in product(Faces, Suits):
print(i)

2.4.5 Russell's Paradox

3. Counting

3.1 Set Size

3.1.1 Basic concepts

The number of elements in a set S is called its size, or cardinality (基数), denoted |B| or # S.

in Python

Size: len, i.e., len({-1, 1})
Sum: sum, i.e., sum({-1, 1})
minimum: min, i.e., min({-1, 1})
maximum: max, i.e., max({-1, 1})

3.1.2 Disjoint

Additional rule (for disjoint):

$A \cap B = \varnothing$: $|A| + |B| = |A \cup B$|
Subtraction rule (for complement):

$A \subseteq B \implies B = A \cup (B - A) \implies |B| = |A| + |B - A|$

3.1.3 General Unions

Principle of Inclusion-Exclusion (PIE)

Two sets

\[ |A \cup B| = |A| + |B| - |A \cap B | \]

Three sets \[ |A \cup B \cup C| = |A| + |B| + |C| - |A \cap B |- |A \cap C| - |B \cap C| + |A \cap B \cap C| \]
n sets

3.1.4 Cartesian Products

Product Rule - the size of a Cartesian Product is the product of the set sizes. (multiplication)

\[ |A \times B| = |A| \times |B| \]

3.1.5 Cartesian Powers

Applications:

Binary strings: $\{0,1\}^n = |\{0,1\}|^n = 2^n$
Subsets

The power set of S, $P(S)$, is the collection of all subsets of S.

\[ P(\{ a, b \}) = \{ \{ \}, \{ a \}, \{ b \}, \{a, b \} \}
\]

The size of the power set is the power of the set size.

\[ |P(S)| = |\{0,1\}|^{|S|} = 2^{|S|} \]

$P(P(S))$ - set of subsets of P(S)

\[ |P(P(S))| = 2^{|P(S)|} = 2^{2^{|S|}} \]
Functions

Functions from A to B: $B^A$, # = $|B|^{|A|}$
- Binary functions
  
  Binary functions of n binary variables: Functions from $\{0 ,1 \}^n $ to $ \{0 ,1 \} $. That is $ \{0,1 \}^{{ \{0,1\} }^{n}} $
  
  #= $2^{2^n}$ Double exponntial
Exponential Growth
- $A^k$: itertools.product(A, repeat = k)
- $n^k$: n**k
```
import itertools 
set(itertools.product({1,2, 3}, repeat = 2))

#Exponent
print(3**2)
```

3.2 Variations

Variable length

Take an example of PIN: #3-5 digit PINs

3.3 Counting trees

Cartesian products as Trees

Trees are more general products

For example, in a university, there are 3 departments, and each department has 2 different courses. Therefore there are 6 courses in total.

Path from Sources to Destination

4 Permutations and combinations

4.1 Permutations

4.1.1 Basic concept and application

n factorial = n!
0! = 1
Stirling's approximation

\[ n! \sim \sqrt{2 \pi n} \left(\frac{n}{e}\right)^n \]

4.1.2 Partial Permutations

permutations of k out of n objects: k-permutaitons of n

$n \cdot (n-1) \cdot (n-2) \cdot \dotsb \cdot(n-k+1) = \frac{n!}{(n-k)!} \newcommand*{\defeq}{\stackrel{\text{def}}{=}} (n)^{\underline{k}}$

kth falling power of n, also denoted $P(n,k)$

4.2 Combinations

Sequences with k 1's

$\binom{[n]}{k} $ - collection of k-subsets of [n] = {1,2,...,n}

corresponds to n-bit sequences with k 1's

two interpretations

Number of n-bit sequences with k 1's: $\binom{n}{k}$

4.2.1 Binomial coefficients

\[ \binom{n}{k} = \frac{n^{\underline{k}}}{k!} = \frac{n!}{k!(n-k)!} \]

$\binom{n}{k} = \binom{n}{n-k}$
recursive: $\binom{n}{k} = \frac{n}{k} \cdot \binom{n-1}{k-1}$

\[ \binom{n}{k} \cdot k = n \cdot \binom{n-1}{k-1}
\]
$\sum\limits_{i=0}^{n} \binom{n}{i} = 2^n$

4.2.2 Binomial Theorem

Pascal's identity

\[ \binom{n+1}{k} = \binom{n}{k} + \binom{n}{k-1}
\]

Pascal's triangle
Binomial Theorem

\[ (a+b)^n = \sum\limits_{i=0}{n} \binom{n}{i}a^{n-i}b^i \]

For example, $(a+b)^4 = a^4 + 4a^3b + 6a^2b^2 + 4ab^3 + b^4$

Think of select # b from n set of {a,b}:

\[ (a+b)^n = \binom{n}{0}a^n + \binom{n}{1}a^{n-1}b + \dots + \binom{n}{n}b^n = \sum\limits_{i=0}^{n}\binom{n}{i}a^{n-i}b^i
\]
- Polynomial coefficient
  
  \[ (1+x)^n = \sum\limits_{i=0}^{n}\binom{n}{i}x^i
  \]
- Taylor expansion
  
  \[ e^x = \sum\limits_{i=0}^{\infty} \frac{x^i}{i!} \]
  
  derived from $(1 + \frac{x}{n})^n = \sum\limits_{i=0}{n} \binom{n}{i} \left(\frac{x}{n}\right)^i$
- Binomial distribution
  
  \[ \sum\limits_{i=0}^{n} \binom{n}{i} p^{n-1}(1-p)^i = (p + (1 - p))^n = 1^n = 1
  \]
4.2.3 Multinomial coefficients

\[ \frac{n!}{k_1! \cdot k_2! \cdot k_3!} \triangleq \binom{n}{k_1, k_2, k_3}, (k_1 + k_2 + k_3 = n) \]
- Multinomial theorem
\[ (a_1 + a_2 + \dots + a_m)^n = \sum\limits_{k_1 + k_2 + \dots + k_m = n \\ k_1, k_2, \dots, k_m \geq 0} \binom{n}{k_1,k_2,\dots, k_m} \prod\limits_{t=1}^{m} a_t^{k_t} \]
- Sum of Multinomialas
\[ m^n = (1 + 1 + \dots + 1)^n = \sum\limits_{k_1 + k_2 + \dots + k_m = n \\ k_1, k_2, \dots, k_m \geq 0} \binom{n}{k_1,k_2,\dots, k_m} \]

4.3 Stars and bars

4.3.1 Basic applications

k terms adding to n

#ways to write n as a sum of k positive integers, when order matters: $\binom{n-1}{k-1}$
Any Sum to n

#ways to write n as a sum of (any # of) positive integers: $2^{n-1} = \sum\limits_{i=0}^{n-1}\binom{n-1}{i}$
Nonnegative terms

#ways to write n as a sum of k nonnegative integers: $\binom{n+k-1}{k-1}$
Simple example

4-letter words (order doesn't matter): #a + #b + ... + #z = 4 $\implies \binom{4+26-1}{26-1} = \binom{29}{25} = \binom{29}{4}$

4.3.2 More applications

#k positive adding to n = #k nonnegative adding to n-k

\[ \binom{n-1}{k-1} = \binom{n-k+(k-1)}{k-1}
\]
#k nonnegative adding to ≤ n = #k+1 nonnegative adding to n

\[ \binom{n+k}{k} = \binom{n+(k+1)-1}{(k+1)-1} \]

need to use Pascal's triangle?

4.4 Python Notebook

Permutation: itertools.permutations(A)
Partial permutation: itertools.permutations(A, k)
Factorial: factorial(len(A)) using the factorial function in math from math import factorial
Combinations: itertools.combinations(A,k)

Week exercise

Use Python to generate a k-composition of an integer n, i.e., a k-tuple of positive integers that sum to n

The simpler way: int(binom(n-1,k-1))
To obtain all the tuples in the composition by define a function:

import sys
import numpy as np
# not clear what the following packages used for
import scipy as sp
from scipy.special import *

def compositions(k, n):
  if k == 1:
      return {(n,)} # (n,) means a tuple containg a single value

  comp = set()
  # comp = [] will generate a list instead of a set.

  for i in range(1, n):  # 1,2,....,n
      for t in compositions(k - 1, n - i): #recursively
          comp.add((i,) + t)

  return comp

5 Topic 5 Probability Introduction

5.1 Basic concept

Random value of outcome, denoted by X.

Probability of random outcome x denoted by P(x) or P(X=x)

Probability distribution function (PDF)

uniform probability space

Toss an unbiased coin or die...
non-uniform probability space

5.2 Three Axioms

Non-negativity $P(A) \geq 0$
Unitarity $P(\Omega) = 1$
Addition rule: A,B disjoint $P(A \cup B)= P(A) + P(B)$

Common problems

1 Problems about counting

Probability that a five-card hand contains

a standard 52-card deck with four suits (Clubs, Diamonds, Hearts, and Spades) and thirteen ranks (2,..., 10, jack, Queen, King, and Ace)

#ways of selecting 5 cards from 52 cards: $\binom{52}{5}$

the ace of diamonds

#ways that the ace of diamonds was selected in 5 cards (i.e., select four other cards from the remaining 51 cards): $1 \times \binom{51}{4}$

$P = \frac{1 \times \binom{51}{4}}{\binom{52}{5}}$
at least an ace

Which is easier to calculate the compensate - counting #ways of no ace: $\binom{48}{5}$

$P = 1 - \frac{\binom{48}{5}}{\binom{52}{5}}$
at least a diamond

#ways of no diamond: $\binom{39}{5}$

$P = 1 - \frac{\binom{39}{5}}{\binom{52}{5}}$
the probability that two cards drawn from a standard deck without replacement have the same rank

#ways of selecting two cards: $\binom{52}{2}$

#ways of selecting two cards in the same rank: $\binom{13}{1}\binom{4}{2}$

$P = \frac{\binom{13}{1}\binom{4}{2}}{\binom{52}{2}}$

Inferential Statistics with Python

Notes from the 2nd course in "Statistics with Python Specialization" on Coursera

Commonly used Python library for inferential statistics

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import statsmodels.api as sm

1 Confidence interval

Example using NHANES dataset.

1.1 One proportion (categorical variables)

\[ \text{confidence interval} = \text{best estimate} \pm \text{mutiplier}*\text{standard error} \]

$\text{standard error} = \sqrt{\frac{\hat{p}(1-\hat{p})}{n}}$
$\text{Best estimate} = \text{sample proportion}$

Method 1 using cross table output

Cross table

One looking at two proportions from two groups, crosstable might be useful pd.crosstable(dx[col1], dx[col2]).

NB: the column names of the cross table are not a list, and thus needs to be renamed by dx.columns = ['col1','col2'] in some cases

Proportion calculation

    dz = dx.groupby(['RIAGENDRx']).agg({'SMQ020x': [lambda x: np.mean(x=="yes"), np.size]})
    dz.columns = ['Proportion', 'Total_n']

Then, calculate p, n, se, respectively

Method 2 using sm library

sm.stats.proportion_confint(prop*n, n, alpha = 0.05)

1.2 Two proportion from two independent variables

\[ \text{confidence interval} = \text{best estimate} \pm \text{mutiplier}*\text{se_diff}
\]

$\text{SE}_1 = \sqrt{\frac{\hat{p}_1(1-\hat{p}_1)}{n_1}}$
$\text{SE}_2 = \sqrt{\frac{\hat{p}_2(1-\hat{p}_2)}{n_2}}$
$\text{se_diff} = \sqrt{SE_1^2 + SE_2^2} = \sqrt{\frac{\hat{p}_1(1-\hat{p}_1)}{n_1} + \frac{\hat{p}_2(1-\hat{p}_2)}{n_2}}$
$\text{Best estimate} = p_1 - p_2$

Calculate lower confidence interval and upper confidence interval respectively. No sm method so far.

1.3 Confidence interval for one mean (quantative variable)

$\text{Best estimate} = \bar{x}$
$\text{Standard error} = \frac{s}{\sqrt{n}}$
- s is the sample standard deviation np.std(data, ddof=1)
- population standard deviation np.std(data, ddof=0)
multiplier depends on the significant level and distribution (z or t). If t distribution, the shape depends on the degree of freedom.
z distribution: sm.stats.DescrStatsW(bmi_female).zconfint_mean()

1.4 Confidence interval for two means from two independent populations

1.4.1 Unpooled approach ($\sigma_1 \neq \sigma_2$)

$\text{Best estimate} = \bar{x}_1 - \bar{x}_2$
$\text{se_diff} = \sqrt{SE_1^2 + SE_2^2} = \sqrt{\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}}$
$df = min(n_1 - 1, n_2 - 1)$ which is a very conservative way or using Welch's approximation

1.4.2 Pooled approach ($\sigma_1 = \sigma_2$)

$\text{Best estimate} = \bar{x}_1 - \bar{x}_2$
$\text{se_diff} = \sqrt{SE_1^2 + SE_2^2} = \sqrt{\frac{(n_1-1)*s_1^2 + (n_2-1)*s_2^2}{n_1+n_2 - 2}}\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}$
$df = n_1 + n_2 - 2$

2 Hypothesis test

General steps:

Set up a Hypothesis $H_0$ and significant level $\alpha$
Check conditions:
- simple random sample?
- nearly normal distribution or sample size large enough
- calculate test statistics (z-score or t)
\[ z = \frac{\text{Best estimate} - \text{hypothesized estimate}}{standard error of estimate}
\]
- find p-value and compare to $\alpha$ and make conclusion - reject $H_0$ or fail to reject $H_0$

2.1 Test on a population proportion

set null hypothesis
- $H_0: p_0$
- $H_A: \hat{p}$
Check conditions: $np \geq 10, n(1-p) \geq 10$
calculate test statistics and p value

\[ z = \frac{\hat{p} - p_0}{\sqrt{\frac{p_0(1-p_0)}{n}}}
\]

se is based on null hypothesis
- traditional method for p value: p_val = 2*dist.norm.cdf(-np.abs(test_stat))
- sm.stats.proportions_ztest()
- sm.stats.binom_test()

2.2 Test on difference in population proportions

set null hypothesis

$H_0: p_1 - p_2 = 0$

$H_A: p_1 - p_2 \neq 0$
Check conditions: $n_1p_1 \geq 10, n_1(1-p_1) \geq 10, n_2p_2 \geq 10, n_2(1-p_2) \geq 10$
calculate test statistics

\[ z = \frac{\hat{p}_1-\hat{p_2}_1 - 0}{\sqrt{\hat{p}(1-\hat{p})(\frac{1}{n_1}+\frac{1}{n_2})}}
\]

se is based on combined the proportion $p = \frac{(n_1p_1 + n_2p_2)}{(n_1+n_2)}$
- traditional method for p value: p_val = 2*dist.norm.cdf(-np.abs(test_stat))
- t test: sm.stats.ttest_ind(population1,population2)
- z score: sm.stats.ztest(population1,population2)
Alternative approaches
1. Chi-square text: different hypothesis and two-side hypothesis
2. Fisher's Exact test
  - allow one-side hypothesis
  - typically for small sample size

2.3 Test on one population mean

set null hypothesis

$H_0: \mu = ?$

$H_A: \mu \neq ?, \mu > ?, \mu < ?$ depending on the research questions
Exam results, check assumptions, summarize data (boxplot, QQplot, Histogram)
calculate test statistics

\[ t = \frac{\bar{x} - \mu}{\frac{s}{\sqrt{n}}}
\]
- s: sample standard deviation np.std(x, ddof=1)
- sm.stats.ztest()
What if normality doesn't hold
- non-parametric test:
  
  e.g. Wilcoxon signed Rank test (use median to do test statistics)

2.4 Test on a difference on population means based on paired data

set null hypothesis

$H_0: \mu_d = 0$

$H_A: \mu_d \neq 0$
Exam results, check assumptions, summarize data (boxplot, QQplot, Histogram)
calculate test statistics

\[ t = \frac{\bar{x}_d - 0}{\frac{s_d}{\sqrt{n}}}
\]
- sm.stats.ztest() or sm.stats.ttest_ind()
- should be in line with the confidence interval inference:
\[ \bar{x}_d \pm t* \frac{s_d}{\sqrt{n}} \]
Normality doesn't hold? - Wilcoxon signed rank est

2.4 Test on a difference on population means based on independent data

set null hypothesis

$H_0: \mu_d = 0 \text{ or } \mu_1 = \mu_2$

$H_A: \mu_d \neq 0 \text{ or } \mu_1 \neq \mu_2$
Exam results, check assumptions, summarize data (boxplot, QQplot, Histogram)
calculate test statistics

\[ t = \frac{(\bar{x}_1 - \bar{x}_2) - 0}{se}
\]
- pooled approach ($\sigma_1^2 \approx \sigma_2^2$) variance
  
  \[ se = \sqrt{\frac{(n_1-1)s_1^2 + (n_2-1)s_2^2}{n_1+n_2 - 2}}\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}
  \]
  
  $df = n_1 + n_2 - 2$
- unpooled approach ($\sigma_1^2 \approx \sigma_2^2$ is not needed)
  
  \[ se = \sqrt{\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}} \]
  
  $df = min(n_1-1,n_2-1)$
- sm.stats.ztest() or sm.stats.ttest_ind()
- sm.stats.CompareMeans(bmi_female, bmi_male).ztest_ind(usevar='pooled')
  
  The argument bmi_female should be the output of sm.stats.DescrStatsW(data)

Data Viz

A list of all the projects I have done in the courses

Data Visualization and Communication with Tableau by Duke University. The link

Increasing Real Estate Management Profits: Harnessing Data Analytics by Duke University This link

Google Data Analytics Certificate This link

English

Speaking English

50 Important Phrasal Verbs

From Speak English with Vanessa

to add up

something that makes sense; usually negative

Her story didn't add up. I think she's lying.
to back (sb) up

to support someone

My parents backed me up when I decided to apply for graduate school.

I've got your back. (I will support you)
to blow up

to become suddenly angry

When I told her I couldn't come to her party, she blew up.
to bring it on

to accept a challenge with confidence

Fifty new phrasal verbs? Yeah, bring it on!
to bring up

to mention in conversation

You shouldn't bring up politics in this house unless you're ready for a long discussion.
to call off

to cancel something that has been planned

Instead of calling off the wedding, the couple decided to elope.
to catch up (on)

to meet with someone you haven't seen in a while

I met my friend for lunch to catch up because we haven't seen each other for a long time.

Wanna meet for coffee and catch up?

I want to catch up on what's happening, so tell me all about it.
to check in

a register a hotel stay

I went to the hotel to check in while my husband parked the car.
to check out

to try sth or to ask sb look at sth with surprise

I'm excited to check out the new park in the city.

Check it out! (Look at this!)
to chip in

to help or contribute money or energy

I couldn't go to the party, but I still wanted to chip in for a gift.

My son likes to chip in and help me with the garden.
to come down with

to become sick but not serious

I'm not feeling so well. I think I'm coming down with something.

Sorry, I think I'm coming down with a cold.
to come up with

to find an idea for something

I need to come up with a great present for my mom's birthday.

I couldn't come up with anything special, so I just baked a cake.
to cut back on

to consume less of something

I'm trying to cut back on fried food, but it's so tasty.

I'm trying to cut back.
to cut off

to end abruptly, usually driving or speaking

The driver in the red car cut me off and almost caused a wreck.
to drop by/in

to stop by for a visit

Hey, are you home? I'm in the neighborhood and I wanted to drop by.

Drop by/in at any time.
to end up

to eventually decide or reach something

We ended up just ordering pizza and not going to the fancy restaurant.

He doesn't want to end up like his father.
to fill in

to provide information usually spoken

I missed the meeting. Can someone fill me in?
to fill out

to write information on a form

Could you please fill out these forms?
to get around (to it)

to delay doing something

I'll get around to that later.

I finally got around to cleaning the garage.
to get back at

get revenge on someone

My sister took my shoes to get back at me for taking her sweater.
to keep on

to continue doing something

If you keep on practicing, you will get better!

Keep on keeping on.
to look out

to watch out for something

When you hike, look out for snakes.

You need to keep an eye out for snakes,
to look uo

to research

I looked it up in the dictionary.
to pull over

to steer the vehicle to the side of the road and stop

It was raining so hard that I had to pull over and wait for the rain to stop.

The police officer pulled me over.

I got pulled over on my way to the party.
to put off

to postpone something

I can't put it off for any longer.
to put up with

to tolerate something or someone

My husband puts up with my terrible singing.

I don't know how he puts up with her! (a little bit harsh)
to run away

to leave or escape

My dog is too lazy to run away.

Did you ever try to run away from home as a kid?
to run into

to meet unexpectedly

I don't want to run into a bear while I'm hiking!

I ran into my high school teacher last week at the grocery store.
to run out (of)

to have nothing left

We ran out of milk yesterday.
to stick with

to continue doing something

I decided to stick with the drums.

Good friends stick with each other even through hard times.
to think over

to consider it seriously

Think it over before you buy a car.
to turn down

to refuse something or someone

I was so full from dinner that I had to turn down dessert.

She turned me down!
to turn off

to stop the flow of something

Some people have trouble turning off their brain before bed.
to turn up

to appear suddenly

My cat was gone for two days. Then he just turned up out of nowhere!
to warm up to

to start liking someone or something

It took my cat a while to warm up to me.

I didn't like the idea at the begining, but I started to warm up to it.
to wear off

to fade away

The energy from my morning tea starts to wear off around noon.

the marker is starting to wear off.
to work (something) out

to come up with a solution or compromise

You guys need to work something out yourself.

Random Variables	Formula	E(X)	var(X)
Bernoulli (p)	\(p_X(x) = \begin{cases} 1, p(x) = p \\ 0, p(x) = 1 - p \end{cases} \)	\(p\)	\(p(1-p)\)
Uniform (a,b)	\(p_X(x) = \frac{1}{b-a}, a ≤ x ≤ b\)	\(\frac{a+b}{2}\)	\(\frac{1}{12}(b-a)(b-a-2)\)
Binomial \(p \in [0,1]\)	\(p_X(k) = \left(\begin{array}{c} n \\ k \end{array} \right)p^k(1-p)^{n-k}, k = 0, 1 ..., n\)	\( np \)	\(np(1-p)\)
Geometric \(0 < p ≤ 1\)	\(p_X(k) = (1-p)^{k-1}p, k = 1,2,3.... \)	\(\frac{1}{p}\)	\(\)

Random Variables	Formula	E(X)	var(X)
Uniform	\(f(x) = \frac{1}{b-a}, a ≤ x ≤ b\)	\(\frac{a+b}{2}\)	\(\frac{(b-a)^2}{12}\)
Exponential \( \lambda > 0 \)	\(f(x) = \begin{cases} \lambda e^{-\lambda x}, x ≥ 0 \\ 0, x < 0 \end{cases}\)	\(\frac{1}{\lambda}\)	\(\frac{1}{\lambda^2}\)

	0 \(1 - \lambda_1\delta\)	1 \(\lambda_1\delta\)	≥ 2 \(O(\delta^2)\)
0 \(1 - \lambda_2\delta\)	\((1-\lambda_1\delta)(1-\lambda_2\delta)\)	\(\lambda_1\delta(1-\lambda_2\delta)\)	-
1 \(\lambda_2\delta\)	\(\lambda_2\delta(1-\lambda_1\delta)\)	\(\lambda_1\lambda_2\delta^2\)	-
≥ 2 \(O(\delta^2)\)	-	-	-